

 |
 |
|
Навигация
|
Главная » Мануалы Так как при t = Q y = h, то dh, и уравнение (6) принимает вид Уравнения y=:h~S. (7) X:=Vat, (3) y--=h--f (7) определяют закон движения камня. Для нахождения уравнения траектории камня исключаем из этой системы время. Траекторией является парабола При интегрировании дифференциального уравнения х = 0 получим: x = Ci. Так как при = 0 x = v, то Ci=v. Следовательно, в любой момент времени i==t<o. (I) Записав jc = и проинтегрировав уравнение (1), получим: x = v,t-C. (2) Так как в момент = 0 л: = 0, то из уравнения (2) следует, что С9 = 0. Таким образом, уравнение (2) можно окончательно записать в виде xv4. (3) Для интегрирования дифференциального уравнения у = - g заменим j) на . Отделив переменные, находим: dSi==-gdt. Проинтегрировав это уравнение, получим y = -gt-rC,. (4) Так как при = 0 р = 0, то из уравнения (4) следует, что Сз = 0, и уравнение (4) принимает вид S)-=~gt. (5) Осуществим последующее интегрирование, предварительно заменив j) на и отделив переменные. Тогда = + a (6) Для нахождения скорости камня в момент падения воспользуемся формулами (1) и (5) проекций его скорости на оси декартовых координат: . = v (1) y = - gi (5) Момент времени Т, соответствующий падению камня на Землю, вычисляем из уравнения (7), учитывая, что при t - Г у = 0. Получим: Следовательно, проекции скорости камня в момент падения даются формулами: XT = Va. j>T=-VWt-Тогда модуль скорости кг мня в момент падения Направляющие косинусы скорости имеют вид: Считая начальную скорость г'о равной нулю, получим из формул (3) и (7) уравнения свободного падения материальной точки в безвоздушном пространстве: х=0. y = h~-l-. Так как х=0, то траекторией точки является вертикалыЕая прямая, совмещенная с осью у. Задача 238. Решить предыдущую задачу с учетом силы сопротивления движению, нропорш-опальной скорости камня: r = - kmv, где т - масса камня, V - его скорость, k - постожшый коэффициент. Определить уравнение траектории камня. Решение. Начальные условия движения камня остаются прежними: при i! = 0 х~, y - h, .v = Do. J = Дальность полета камня определяется его абсциссой в момент падения на Землю. Подставив в уравнение (8) у = 0, определим дальность полета: К камню М приложены две силы: Р -вес камня, R - сила сопро-тивленнм движению, нанравленнач но касательной к траектории в данной точке в сторону, противоноложную движению. 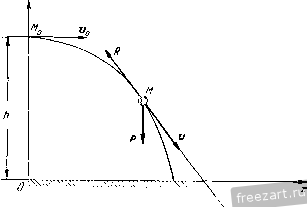 К задаче 238. Составим векторное дифференциальное уравнение движения камня: mw .= P-\-R, но так как w - r и R - - mkv = - ткг, то получим Проектируя на оси х и у, имеем: х = -/сх, y = -g-ky. (1) 1 ак как X - , то lnx=z!d-\- Cj. Постоянная C находится путем использования начального условия движения (=0, X = !)(,). что дает C = lnx o- Следовательно, In = - kt, xv,e- . Проинтегрировав уравнение (2), находим: Тогда ln(/j+) = +C:,. Использовав начальное условие движения (при t = 0 у = 0), найдем, что Сз - - In g. Следовательно, y-.= le- ~l. (4) Заменив в уравнении (4) у на и интегрируя это уравнение, получим: ~k ~ к- . - 1 V - - - е - с, Так как при t = 0 y - h, то Ci = h-\~ и, следовательно, = /г- - + Л1-е-*). (5) Итак, камень совершает движение сог.тасно уравнениям: .v = ;([-e-*a (3) J = /-f + (Г.) Исключив время из системы (3) и (5), определяем уравнение траектории камня: При движе1ши с малой скоростью сила сопротивления пропорциональна первой степени скорости точки. Движению материальной причем так как при t = 0 х = 0, то d - . Итак, х==;(1-с-*). (3) Для решения второго дифференциального уравнения (1) заменим у на - и отделим переменные: точки со значительной скоростью соответствует сила сопротивления, пропорциональная квадрату скорости (см. задачу 239). Задача 239. Сохраняя условие задачи 237 с учетом силы сопротивления движению, пропорциональной квадрату скорости камня: R = ktnv, где т - масса камня, т - его скорость, k - ностоянн1,1й коэффициент, определить уравнение участка MoMi траектории камня, непосредственно примыкающего к его начальному положению М^. 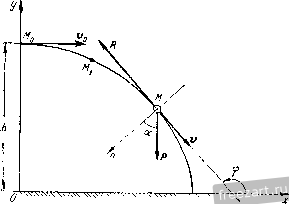 К задаче 239. Решение. Начальные условия движения камня остаются прежними: при = 0 х=0, y - h, x=Vo, у - О. Направления сил Р и /? не изменились по сравнению с предыдущей задачей. Поэтому /? = - kmvv = - kmvr. Запишем векторное дифференциальное уравнение движения камня: или ? = g~kvr. проектируя на оси л- и у, получим: х = - kvx, ( I ) у= -g--AwJ>. (2) 56 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДИНАМИКИ ТОЧКИ [ГП. VIH Для интегрирования дифференциального уравнения (1) заменим X на а V па, где а-дуговая координата, измеряемая по траектории от точки М^. После отделения переменных получим: = - Л da, lux = - ko-\-C. (3) В начальном положении камня, т. е. при а = 0, проекция скорости .v = T o. Слеловагслыю, C~\nva. Подставив это значение С в уравнение (3), находим: In - = - ка, х^г^- (4) Для упрощения репшния задачи вместо диферспниального ур/ап-псния (2) воспользуемся дифференциалыплм уравнением движения камня в проекции иа (лавпую нормаль п: т - - = Pcos а Р (сила сонро!ивлсния r даст проекцию на главную нормаль, равную пулю). Так как а=:2т: - <f, -де 9 - угол между осью х и касательной, то cosa=:cos9, т. е. rTcOSCS. (5) Как известно из курса дифференциальной геометрии, кривизна кривой н данной точке Знак минус взят потому, что с возрастанием а угол 9 убывает. Так как tgf=yjc, то 9-aictg/j. Следовательно, d-o d . , ,. \ dx tf, = -(arcto.)=nf7/-.V.--rf-. Учитывая, что do-\\-\-y[dx, находим: -= (Это-~- выражепие кривизны кривой, известное из курса дифференциальной геометрии.) -р- = -J/Icos. (7) Воспользовавшись формулой (7), перепишем уравнение (5) в виде: -. .; v- cos- 0 = - р-. dx- Учитывая, что T)COSf = jc, а также формулу (4), получим: =-с'->\ (8) dx- vl По условию задачи требуется определить уравнение настильного участка траектории М^М^, непос[)елственно прилегающего к начальному положению точки Л1о. Так как этот участок траектории близок к горизонтальному, то, считая а величиной первого порядка малости, мы можем с точностью до слагаемых первого порядка малости вклю-1ительно замевшть в уравнении (8) а на х (разность х - а является величиной второго порядка малости). Теперь диф()еренниа.тьное уравнешю (8) принимает вид dx- а- Проинтегрировав это приближенное диф()срснниальное уравнение, находим: dx Ikv При л: = 0 = 0 (касательная к траектории в точке ЛГо расположена горизонтально). Подставив эти начальные ус.товия в уравнение (10), находим, что С|=г^:,. С.чедоватсльно, уравнение (10) при1шмает вид dx~~2kv- 2kvf > Проинтегрировав дифференциальное уравнение (11), получаем: Подставив получетюе значение - в формулу (6), имеем: 1 Л'; -V.; Так как при х = 0 у = И, го С =/г--, и уравнение (12) принимает вид . (1 е^*). Это - искомое приближенное уравнение участка траектории Задача 240. Материальная точка М движется в вертикальной плоскости под действием центральной силы притяжения, пропорцио- 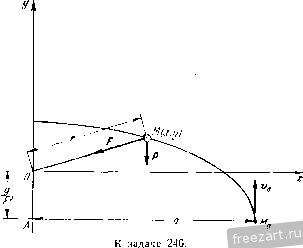 нальной ее расстоянию до неподвижного центра: F= - kmr, где г-вектор-радиус точки, т-ее масса, - постоянный коэффициент. Найти уравнение траектории точки, если в начальный момент она за- нимала положение Жо 1а, - и имела скорость v, направленную по вертикали вверх (см. рисунок). Решение. Начало осей декартовых координат взято в неподвижном центре О, к которому притягивается точка М. Ось х проходит но горизонтали направо, ось у - по вертикали вверх. За[шшем начальные условия движения точки в виде: при = 0 х - а, у = - x - Q,ji=:v. К материальной точке М приложены следующие силы: Я - ее вес, F-сила притяжс1шя, направлешшя к неподвижному центру О- Составим векторное дифференциальное уравнение движения материальной точки mw=pf или Проектируя на оси хну, получим: x-[-kx = 0, (1) yklv = ~-g. (9) Уравнение (1) является однородным линей1н.1М дифференциальным уравнением второго порядка с постояеншши коэффициентами. Для его интегрирования составим характеристическое уравнение Xk = 0; откуда Х] 2=- ki. Следовательно, общее решение дифференциального уравнения (1) запишется в виде x=Ci cos kt -j- Q sin kt, (3) где C и Q-постоя1Шые интегрирования. Для определения Ci и Са вычислим х = - Cik i\n kt-]-Ck cos kt (4) и затем подставим в уравнение (3) t = 0, х = а, а в уравнение (4) t = 0, х = 0. Находим: С|=а, С^О. Внося эти значения Cj и в уравнение (3), имеем: х = а cos kt. (5) Дифференциальное уравнение (2), в отличие от диффереициального уравнения (1), является неоднородным. Следовательно, eio обн1,ее решение имеет вид У=У1+Уь (6) тле уг - частное решение неоднородного уравнения, а з', - общее решение соогветстнующего однородного уравнения: у -ky = 0. (7) Заметив, что диффере1Щиальное уравнение (7) аналогично дифференциальному уравнению (1), запишем: y =z Сз cos kt -f Ci sin kt. (8) Правая часть дифференциального уравнения (2) постоянна. Поэтому ищем частое решение в виде 3/5:= Л, где А - постоянная. Положив в уравнении (2)у = А, находим: Воспользовавшись формулами (8) и (9), запишем общее решение по формуле (6): yCicos/d -f Qsinlt~-l,. (10) Для определения постоянных интегрирования Q и Q вычислим: J = -Q*sinA-l-Ci cos ЛЛ (11) Затем подставим в уравпепие (10) f = 0, j/ = - а в уравнение (11) i - Q,y = v. Тогда Ci = 0, Ci~ ~. Подставив эти значения C;i и Q в уравнение (10), получим: y = -imki~-,. (12) Итак, уравнения движения материальной точки имеют вид -с = а cos kt, ysinkt-Я. Для определения уравнения траектории следует из уравнений движения исключить время. Замечая, что cos/;i=-, smM==-(y-fX получим искомое уравнениб' траектории / ,= (Эю - уравнение эллипса с центром в точке а(о, -jj. Одна полуось эллипса равна а, а другая полуось равна . Задача 241. Материальная точка движется в вертикальной плоскости ПОД действием центральной силы отталкивагшя, пропорциональной расстоянию до неподвижного центра: fkmr, где г - вектор-))адиус точки М, т - ее масса, k - постоянный коэффициент. Пайти уравнение траектории точки, если в начальный momcit: она занимала положение Afj (C.)A1q = ) и имела скорость Hq, паправлен-пую но юризонтали направо (см, рисунок). Решение. Начало декартовых осей координат взято в неподвижном центре С), or которого отталкивае!ся точка Л/. Ось х проходит но горизошали направо, ось - через начальное положение 1 2 3 4 5 6 7 8 ... 66 |
 |
 |