

 |
 |
|
Навигация
|
Главная » Мануалы точки по вертикали вверх. Запишем начальные условия движения точки в виде: при t = Q х= О, y = b, х = а„, J) = 0. К материальной точке М приложены следующие силы: Р - ее вес, F-сила отталкивания, направленная вдоль ОМ от центра О. 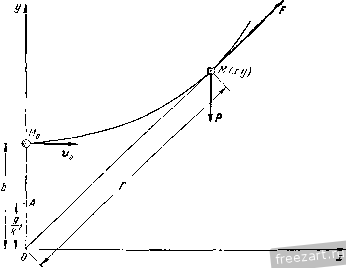 К задаче 2-11. Составим векторное дифференциальное уравнение движения материальной точки: mw =-P-F, или Проектируя на оси х и у, получим: Jc r-jc = 0, y-ky=-g. (1) (2) Уравнение (1) является однородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. Для его интегрирования составим характеристическое урапиение; л' - А^ = 0, откуда а, ,j = zLA. Следовательно, решение дифференциального уравнения (1) запи1нет.:я в виде xQe-Cc Для определения постоянных интегрирования Q и Cj вычислим x=Cike - dke- (4) и затем подставим в уравнение (3) = 0, д;=:0, а в уравнение (4) t = Q, x = va. Тогда получаем систему уравнений: 0=:Cl+Q, Vg=Clk - dk. Решив эту систему, имеем: Ci = и 0, = - Следовательно, окончательно получим: x = ll (й* - е- ) = sh kt. (5) Так как дифференциальное уравнение (2) является неоднородным, то его общее решение у имеет вид У=У1-\-Уъ (6) где у,-общее решение соответствующего однородного уравнения: y-ky = 0 (7) ч Уч - частное решение уравнения (2). Дифференциальные уравнения (1) и (7) аналогичны, поэтому yi = Qe Cie-. (8) Правая часть дифференв,иального уравнения (2) постоянна. Поэтому частное решение 3/3 иитем в виде постоянного: 3/3= Л. Положив в уравнении {2) у^= А, находим: У. = 1,- (9) Воспользовавшись формулами (8) и (9), запишем общее pemeime по формуле (6): j;=(V-f С4.-*+. (10) Для определения постоянных интегрирования Сз и d вычислим: y = C3ke -dke- . (11) Затем подставим в уравнение (Ю) t = 0, у - Ь, а в уравнение (11) = 0, j> = 0. Тогда получим систему уравнений: О = СзА - dk, Окончательно: т. е. (12) Итак, уравнения движения материальной точки имеют вид: х= ° sli kt, k yib-f \chkt (5) (12) Для определения уравнения траектории точки следует из уравнений движения исключить время. Из (5) и (12) находим: sh kt= - , о ch kt= Учитывая, что chkt - s]ikt=l, получаем искомое уравнение траектории точки М: Это - уравнение гиперболы с центром в точке Л ствительная полуось равна b - < з мнимая полуось . Задача 242. Найти наибольшую высоту подъема над поверхностью Земли снаряда, вылетевшего с начальной скоростью Ио под утлом а к горизонту и упавшего на Землю, считая силу притяжения Земли обратно пропорциональной квадрату расстояния до центра Земли. Силой сопротивления- д1И1жению пренебречь. Снаряд считать точечной массой. На поверхности Земли ускоре1ше силы тяжести равно g. Радиус Земли равен R. Решение. Предположим, что снаряд в рассматриваемый произвольный момент времегш находится в точке М (см. рисунок), а в начальный момент времени находился в точке М^. Учитывая, что к снаряду приложена только центральная сила f, решаем аадачу в полярных координатах. Полюс О выбираем в центре Земли, оси г даем направление вектор-радиуса ОМ от О к Ж. Ось 9 проводим через точку М перпендикулярно к оси г. Оси Го и 90 соответствуют начальному положению снаряда М^. 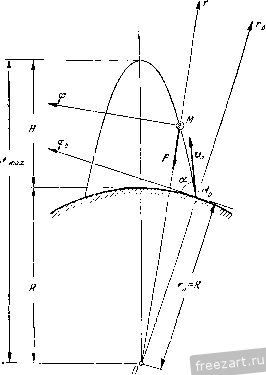 К задаче 242. Запишем начальные условия движения снаряда в виде: при =0 г = Гй = Я, 0 = 0, r = v = Va sin а, Фв = cos а. Действительно, если обозначить начальное значение 9 через 90. то нр.Фо = 090. а вследствие соотношешш np.jio -iij cos я 11аходт;м: /<fo = o COS я, f=-.. Сила притяжения f направлена к центру О. Дифференциальные уравнении движения материальной точки в проекциях на оси полярных координат имеют вид: mi?-r) = F.. !l(r-) = F,. В дагшом случае Следовательно: ?-Г9-. (3) -7С^Т) = 0. (4) Из дифференциального уравнения (4) следует интеграл площадей: г'! = С, т. е. г'=4ъ- (5) Учитывая, что Го = /?, а также формулу (1), запишем формулу (5) в виде г^ф =: Rv cos а, {г'& является удвоенной секториальной скоростью снаряда, т. е. производной по времени от площади, описываемой вектор-радиусом г снаряда. Итак, при центральном движении материальной точки ее секториальная скорость постоянна). Обратимся к интегрированию дифференциального урапне1шя (3). Воспользовавшись формулой (6), запишем это уравнение в виде r , - . 3 Теоретическая механика, тон II откуда следует записанное выше: ?о = - COS а. К снаряду приложена только сила притяжения f, обратно про- klfl порциональная квадрату расстояния до центра Земли, т. е. F=-. Учитывая, что на поверхности Земли, т. е. при r = R, F=P=tng, находим, что k = gR. Следовательно, Следовательно, Уравнение (7) устанавливает зависимость между проекцией скорости снаряда f иа ось г и радиусом-вектором г. В наивысшей точке траектории проекция скорости снаряда на ось г равна нулю, т. е. при г=Гтлх f = 0. Подставив эти значения в уравнение (7), получим квадратное уравнение относительно Гтл^: {IgR - v;) r - Шгш.. + Rvlzoa. = О, eR±L YgR--{2gR-vl)vl cos<>. , Гтах- IgR-vl Из уравнения (8) следует, что при vl = 1gR величина Гтг\ обращается в бесконечность, т. е. снаряд па Землю не возвратится (va = V1gR = = 11,2 км/сек называется tsTopoH космической скоростью). Поэтому снаряду надо сообщить начальную скорость, удовлетворяющую условию 2gR - viyO. т. е. Vo<V2gR. Наибольшая высота подъема снаряда над поверхностью Земли Использовав формулу (8), получи.м: --].-R- (9) Отбрасывая отрицательное значение Н^, окончательно находим: --- Wi - Для случая, когда начальная скорость направлена по вертикали вверх, т. е. при (i= ~, имеем: - 2gR-vy Умножив почленно на dr, осуществим интегрирование, учитывая, что ?dr=~dr = fdf. dt Получим: 2 Г - -~+ Так как в начальном положении снаряда r = ra = R, r = npVf,= - z/o sin a, TO постоянная интегрирования имеет вид 2gR-vl 2 / I R41 zc-о. gR 2gR - vl 2 I 2r - ~Г 2 Задача 243. 4 октября 1957 г. в Советском Союзе был запущен первый в мире искусственный спутник Земли. В момент выведения на орбиту в положении на высоте h спутник имел скорость щ, расположенную под углом а к вертикали, проходящей через центр Земли. Требуется показать, ito спутник движется по эллипсу. Сила зем1Юго притяжения обратно пропорциональна квадрату расстояния 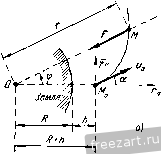 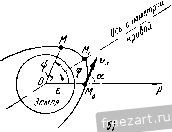  да* йг. с пимметрии злпипса Р К задаче 243. спутника от центра Земли. Ускорение силы тяжести на поверхности Земли равно g. Радиус Земли R. Силой сонротивления движению нренебре1ь. Решение. Так как начальная скорость ф и сила земного притяжения F лежат в одной плоскости, то траектория спутника является плоской кривой. Поэтому выберем систему полярных координат с полюсом О в центре Земли (рис. а). Радиус-вектор ОМ. соединяет полюс О с промежуточным положением М движущегося спутника. Вдоль ОМ проводим ось г, а перпендикулярно к ней через точку М - ось 9. УИо - начальное положение спутника на орбите. Из условия задачи видно, что начальные условия движения спутника имеют вид: ри = 0 r = r = Rh, 9 = 0, г = и = Фа о = г^и cos а, 90 = sin а, о 68 дифференциальные УРАВЕ1ЕНИЯ динамики точки (ГЛ. viii ибо, если обозначить начальное значение 9 через 90. то прфд = Гофц, и вследствие соотношения прФо = z;o sin а находим: .)9o = Jo sin а, (1) т. е. 9о является заданной величиной. Движение спутника М происходит под действием центральной силы f земного притяжения, направленной к центру Земли. Сила земного притяжения обратно пропорциональна квадрату расстояния до центра Земли, т. е. =7-. (2) На поверхности Земли, т. е. при r = R, F=P=ing. Подставив эти значения в формулу (2), находим, что k = gR. Следовательно, формула (2) принимает вид F=. (3) Составим дифференциальные уравнения движения спутника в полярных координатах. Учитывая, что дифференциальные уравнения движения материальной точки в полярных координатах имеют вид: m{?~r) = F !}(гЦ) = Р в данном случае получим: ni{r-rf) = -F, (г^9) = 0 или, принимая во внимание формулу (3): ? гф = -, И) ~(г') = 0. (5) Из дифференциального уравнения (5) находим: г^9=С. (6) Так как секториальная скорость точки, т. е. производная по времени от площади 5, описываемой вектор-радиусом г, равна S = 9 C=2S. Итак, секториальная скорость спутника постоянна, т. е. г^9 = ГдФо. Воспользовавшись формулой (1), запишем формулу (6) в виде С= гЦ = rjcfо - flosin а, . гл- (7) S 31 ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ ПО ЗАДАННЫМ СИЛАМ 69 Переходим к исследованию дифференциального уравнения (4): Вычислим производную от г по времени: / = -9. Учитывая формулу (7), находим: dr Го о sin а . d f ] \ Так как ? = = 9, то, воспользовавшись формулами (7) и (8), имеем: г,X sin а rf2 / 1 Запишем дифференциальное уравнение (4) с учетом формул (7) и (9). Тогда Ф1 sin а d f \ \ rlvf, Sin а gfi- Г- df\r! Н ~ г- $(-;-)+-:=А где rjjjjsin-a- Проинтегрировав дифференциальное уравнение (Ю), мы определим искомое уравнение траектории спуышка в полярных координатах. (Дифференциальное уравнение (10) можно было непосредственно получить, воспользовавшись формулой Бине: dfXrj Г тС где С-удвоенная секториальная скорость: С= 2.5= Гог)о sin а, а Уравнение (10) является неоднородным линейным дифференциальным уравнением относительно у с постояшгыми коэффициентами. Его 1 / 1 общее решение - равно сумме общего решения -соответствующего однородного уравнения (12) Для решения дифференциального уравнения (11) составляем характеристическое уравнение >.--1=0, откуда \ = ±i. Следовательно, \ = Бсо5(9-е). (13) где S и е - постоянные интегрирования, подлежащие последующему определению. Нетрудно видеть, что частное решение дифференциального уравнения (10) равно его постоянной правой части, т. е. (14) Воспольяовавшись формулами (13) и (14), запишем общее решение по формуле (12) в. виде - = 5 cos (9 - е) Ц- Л. (15) Это уравнение является уравнением траектории спутника. Для определения постоянных интегрирования Z? и е вычислим производную от у по времени: р г == - 9 sin (9 - е). Подставив в уравнение (15) г = rf, = R-\~h, <р = 0, а в уравнение (16) г = Го = R -г Л. 9 = 0. r = r = vcos л, v sin а v sin а получим систему уравнений: /==Scoss+X, Оц cos а Rv .sin а R+h sm е. (17) Для определения постоянных интегрирования В и s из уравнений (17) запишем эту систему в виде: В cos е = jS sin е = R + h otga R + h (18) (19) и частного решения неоднородного уравнения, т. е. 1 ... 3 4 5 6 7 8 9 ... 66 |
 |
 |