

 |
 |
|
Навигация
|
Главная » Мануалы § 3 ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ ПО ЗАДА1ИШМ СИЛАМ 71 Из системы (18) и (19) находим: или, подставляя значение А, после несложных преобразований: -,. + 4C;.in.y --gfrW-C/T (20) Разделив (19) на (18), находим tg е и, следовательно, s = arctg- + i cosa Вернемся к уравнению траектории спутника, записанному в виде (15). Решив это уравнение относительно г, находим: 1 ДС08(<? - е) или где [R-\-hYvl sina л-- g;.- . (2.i) . = -J- = / i-igl2/- (; (24) ф=9-Е. C->5) Здесь £ определяется по формуле (21). Как известно из курса аналитической геометрии, уравнение (22) является уравнением кривых второго порядка в полярных координатах. В нем р-параметр кривой, а е - эксцентриситет. Кривая является: а) окружностью при e - Q\ б) эллипсом ири е<\; в) параболой при е=\\ г) гиперболой при е'Х. Угол (jj отсчитывается от oc;i симметрии кривой до радиуса-вектора, определяющего положение точки М на кривой (см. рис. 6), причем ось симметрии направлена от полюса О (в данном случае центра Земли), находящегося в одном из фокусов кривой, в сторону ближайшей к фокусу вершины. Угол е определяет положение оси симметрии кривой. Выясним характер начальны; условий запуска спутника для того, чтобы он мог двигаться но каждой из этих кривых: а) Для того чтобы спутник двигался по окружности, должно бьыь выполнено условие е = 0, т. е., согласно формуле (24), 1 - + % PsR - W + /О ьП<1. Для выполнения этого неравенства необходимо, чтобы Итак, ДЛЯ того чтобы движение спутника происходило по эллипсу, его начальная скорость на орбите должна удовлетворять условию Однако этого условия недостаточно, так как эллиптическая траектория спутника не должна проходить внутри Земли. Значит, наименьшее расстояние г должно быть больше или равно радиусу Земли R, т. е. Гшш^/?. (28) Расстояние от фокуса О, совмещенного с центром Земли, до точки на эллипсе является кратчайшим в момент прохождения спутником положения Ml (см. рис. б), т. е. при ф = 0. Поэтому, подставив в неравенство (28) значение г из уравнения (22) и считая при этом ф = О, получим: откуда получаем биквадратное уравнение относительно начальной скорости спутника на орбите: (R + hf vl sin a - 2gR (R + h) vl sin a + gR = 0, T. e. Комплексное знамение vl указывает, что движение спутннка по круговой орбите возможно только в частном случае, когда а=-, т. е. при горизонтальном направлении начальной скорости v. Тогда (Эта формула получена выше, в задаче 220.) б) Для того чтобы спутник двигался по эллипсу, должно быть выполнено условие е<[1. т. е., согласно формуле (24), VgR-7T&T.l/--г- , . Х2 (30) Сопоставив неравенства (27) и (30), видим, что условие, при выполнении которого спутник будет двигаться вокруг Земли по эллиптической орбите, можно записать в форме y2gR- I/ lP-Lh\ cin3 I , где -Do - начальная скорость спутника на орбите; h-начальная высота спутника над поверхностью Земли; g-ускорение силы тяжести у поверхности Земли; а - угол, образуемый начальной скоростью с вертикалью. Для вещественности левой части неравенства (31) необходимо, чтобы sm а R + fi- При запуске спутника с поверхности Земли, т. е. при h = 0, получаем, что I sin а 1=1, т. е. а = у или а = у (см. рис. в). Однако в этом случае левая часть неравенства (31) принимает неопределенный вид . Полагая в левой части (31) lsinal=l и затем устремляя li к нулю, приходим к неравенству /gRv,-< V. (32) Полагая g-=9,81 м/сек^ и /? = 6370 км, имее.м: 7,9 км/сек Vo<;\l,2 км/сек. (33) Итак, при запуске с поверхности Земли для движения спутника по эллиптической орбите модуль его начальной скорости должен удовлетворять неравенству (33), причем начальная скорость должна быть направлена горизонтально. Значение v=7,9 км/сек называется первой космической скоростью, а значение = 11,2/сл/сйк называется второй космической скоростью. В случае и„<[7,9 кмсек тело падает на Землю. в) Для того чтобы тело двигалось по параболе, должно быть выполнено условие е=]. Из формз'лы (24) следует, что при е=\ 2erR -(R + 0 = 0, откуда Подставив в неравенство (29) значение величин р и е, т формул (23) и (24) найдем после ряда преобразований: г) Для того чтобы тело двигалось по гиперболе, должно быть выполнено условие откуда следует, что Из формул (34) и (35) следует, что при (35) (36) тело будет двигаться по параболе или гиперболе, т. е. не окажется спутииком Земли и будет от нее бесконечно удаляться. Если, кроме того, в начальный момент тело находится на поверхности Земли, т. е. /г = 0, то из фор.мулы (36) получим: 11,2 км/сек. (37) (38) § 4. Колебательное движение 1°. Восстанавливающая сила. Теория колебаний является одним из важнейших разделов теоретической механики. Ее роль в современной технике все время возрастает. При проектировании двигателей, машин и механизмов, мостов и других сооруже1Щй всегда производятся расчеты на колебания. В данном параграфе рассматривается простейшая задача о линейных колебаниях материальной точки (крутильные колебания рассмотрены ниже в главе IX, малые колебания систем материальных точек - в главе XIII). Линейными называются колебания, описываемые линейными дифференциальными уравнениями. При движении материальной точки может действовать упругая сила, стремящаяся вернуть точку к некоторому положению. Эта упругая сила называется восстанавливающей. В большинстве задач рассматривается восстанавливающая сила f, изменяющаяся по линейному закону (по закону Гука) (рис. 111). При растяжении пружины эта сила прямо пропорциональна удлинению 7=-сД, где А - смещение конца пружины из ненапряженного состояния, с - коэффициент упругости {коэффициент жесткости), численно равный силе, которую 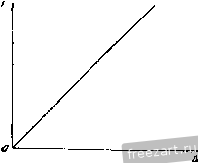 Рис. III. Рис. 112, 2 . Свободные колебания материальной точки. Свободными называются колебания материальной точки, которые происходят под действием восстанавливающей силы. При движении материальной точки М массы т. по гори.зонтальной оси х (рис. 112) под действием восстанавливающей силы f, равной по \\\\ч\\\\\ модулю F = c\x\ {О-положение равновесия точ- ки уИ), имеет место дифференциалыюе уравнение движения xkx О, где Д^ = - . т В случае колебаний материальной точки М массы т, подветенной к нижнему концу пружины, верхний конец которой прикреплен к потолку, упругая (восстанавливающая) сила f при движении точки М вниз направлена вверх (рис. 113), причем Рх- - с(Дст + ). где Дет - статическое удлинение пружины под дейст-иием силы веса P=mg. Ось х Егзправлена вдоль оси пружины в сторону ее растяжения, т. е. вниз. Начало отсчета на оси взято в положении статического равно- Рис. 113. весия материальной точки М, висящей на пружине. При этом выборе начала отсчета дифференциальное уравнение свобод[1ЫХ колебаний материальной точки имеет вид где k = - . т При начальных условиях движения материальной точки, записанных в виде: при / = 0 х~х„, х = х^, закон ее свободных колебаний имеет вид х-а sin {kt-\-a% надо приложить к пружине для того, чтобы изменить ее длину на единицу. Единица измерения коэффициента упругости-кг/см. Вообще линейной восстанавливающей называется сила, стремящаяся вернуть точку в положение равновесия и пропорциональная отклонению этой точки от положения равновесия. О F М I . -Г i, kt-\-a. - фаза колебаний, а - начальная фаза колебаний, определяемая по начальным данным: k - круговая частота колебаний - число колебаний материальной точки за 2i: секунд: Круговая частота колебаний от начальных условий движения {х^ и х^ не зависит. Это свойство называется изохронностью, а колебания - изохронными (амплитуда колебаний а и начальная фаза а зависят от начальных условий движе1щя). Периодом колебаний Т материальной точки называется наименьший промежуток време1И1, по истечении которого точка имеет ту же координату и ту же проекцию скорости Размахом колебаний называется расстояние между крайЕвтми положениями колеблющейся точки. Размах колебаний равен двум амплитудам колебаний. 3°. Влияние силы сопротивления, пропорциональной скорости, на свободные колебания материальной точки. При движевши материальной точки в среде, препятствующей движению (воздух, жидкость), возникает сила сопротивления движению. Эта сила при малых скоростях движения точки можег приближенно считаться прямо пропорциональной первой cTcneim скорости точки: n = v, где (i - постоянный коэффициент; при больших скоростях - квадрату скорости точки: J = v, где j3,-постоянный коэффициент. Ниже рассмотрены свободные колебания материальной точки при наличии силы, пропорциональной первой степени скорости точки: R=v. В этом случае дифференциальное уравнение движения материальной точки имеет вид x-2nx-kx = Q, где Т. е. материальная точка совершает гармоническое колебательное движение; здесь а - амплитуда колебаний - наибольшее отклоняйте колеблющейся точки от положения равновесия о ft -;Н в д„4-ил- Это движение не является периодическим, так как выражение Ле переменно и убывает по экспоненциальному закону. Однако по аналогии со свободными колебаниями и здесь вводят круговую частоту и период колебаний. Круговая частота колебаний Л/? материальной точки при наличии силы сопротивления равна т. е. kif<k. Итак, сила сопротивления движению, пропорциональная скорости, уменьшает круговую частоту колебаний. Период колебаний Т/ материальной точки при наличии силы сопротивления, пропорциональной скорости, равен у, 2к 27t Так как при отсутствии силы сопротивления Г= , то т. е. 7 ;; Т. Итак, сила сопротивления, пропорциональная скорости, увеличивает период колебаний. Обычно условно вводят переменную амплитуду колебаний а = Лe~ представляющую, по существу, величину наибольшего отклонения. Амплитуда колебаний а = Ае (при -.оо а-0) убывает с каждым полупериодом (см. рис. П4) по закону геометрической прогрессии, знаменатель которой равен пТп а; Различаются три вида движения: а) n<k - случай малого сопротивления, б) п^А - случай большого сопрот1шления, в) n = k - предельный случай. а) n<k - случай малого сопротивления. Материальная точка совершает затухающие колебания но закону: X Ас- sin (/А' - и' t + а) (при f-co л: -0). При заданных начальных условиях движения (при = 0 х = Х(, х - Хо) А и а имеют вид Логарифмическим декрементом колебаний называется логарифм ог-ношения двух смежных амплитуд, отличающихся во времени па т. е: i+l б) nk - случай большого сопротивления. Материальная точка совершает затухающее апериодическое (непериодическое) движение согласно уравнению При -►оо JC-*0. Вследствие изменения по показательному закону движение быстро затухает.
Рис. 114. При заданных начальных условиях движения: при = 0 Х - Х^, X = ±ss, постоянные интегрирования имеют вид: 4- ( + / - fe) X, sc,\{n-yn к') х„ или .-nt 2Yn - ft [x,i-{n-/n~k)x,]e -[x, + (n-Vn->)x,\e x = -S-Z.- [(Л-0 -L nxo) sh /n - -f jto /л^ - k ch /n - A /]. У - fe Характер движения зависит от начальных условий. При х=:Х(0 х -ХцО, т. е. когда в начальный момент материальная точка 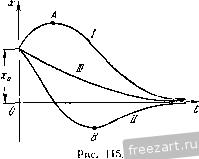 смешена из положения статического равновесия на лгд и ей сообш,ена начальная скорость в том же направлении, материальная точка вначале отклоняется в указанном направлении до точки А (см. на рис. 115 кривую /), а затем асимптотически приближается к положению равновесия (не переходя через него). При д: = хо>0 x = JCo<0 (причем хо>л:о(/г+ /и^ -А*)), т. е. когда в начальный момент материальная точка смещена из положения статического равновесия на и ей сообщена в противоположном направлегши скорость, модуль которой удовлетворяет указанному выше неравенству, материальная точка приближается к положению равновесия, проходит его (см. на рис. 115 кривую ), отклоняется в противоположную' сторону до точки в и затем асимптотически приближается к положению равновесия (больше не переходя через него). Прп х = л:о^О x = Xi; (причем I Хо I <л: (й-- ]/л' - k)), т. е. когда в начальный момент материальная точка смещена из положения равновесия на Xq и отпущена без начальной скорости, либо ей сообщена в противоположном направлении начальная скорость, модуль которой удовлетворяет указанному неравенству, материальная точка асимптотически приближается к положению равновесия, не переходя через него (см. кривую /). Во всех трех случаях движение быстро затухает. в) п = А - предельный случай. Материальная точка совершает затухающее апериодическое движение: х - е'С^-у С4\ При С -оо X становится неопределенностью типа О оо. Раскрытие неопределенности по правилу Лопиталя дает ]1тл:=0, что указывает на затуха- ние движения. При заданных начальных условиях движения < = 0 X - Xi, х = х, уравнение движения имеет вид x = e-\x-\ix,nx)t\ Характер затухания зависит от начальных условий движения. При х = Хпо x = XqO движение материальной точки соответствует кривой /. При х = Хао, х = Хо<0 (причем J >nxo) движение материальной точки соответствует кривой . При д: = л;о^О, x=X(f=0 либо JCo<CO (причем \Хо\<пхо) движение материальной точки соответствует кривой /. Во всех трех случаях движение быстро затухает. Решение задач на свободные колебания материальной точки рекомендуется выполнять в следующем порядке: 1) выбрать систему отсчета, взяв начало Отсчета в положении статического равновесия материальной точки; 2) записать начальные условия движения материальной точки; 3) изобразить на рисунке задаваемые силы, приложенные к материальной точке. Применив пригщип освобождаемости от связей, добавить силы реакщ1й связей; 4) составить дпфферегшиальное уравнение движения материальной точки в проекции на соответствующую ось; 5) проинтегрировать дифференциальное уравнение движения, использовав начальные условия движения для определения постоянных интегрирования. Для определения круговой частоты k и kf и периода колебаний 7 и Tff нет необходимости в интегрировании дифференциального урав-не1шя движения. Достаточно, составив диффере1Щиальное уравнение движения, определить коэффициент А' при координате, коэффициент 2я при проекщш скорости х точки и вычислить круговую частоту и период колебаний по указаншлм выше формулам. При составлении диффере1Щиального уравнения надо изобразить материальную точку в промежуточном положении, соответствующем ее положительной координате, предположив при этом, что точка перемещается в сторону возрастания этой координаты. После составления дифференциального уравнения движения (nyiHCT 4) следует рассмотреть условие статического равновесия материальной точки, совершающей колебания. Использовав это условие, часто удается сократить ряд постоянных слагаемых в правой части дифференциального уравнения. Рассматривая задачу о СЕободных колебаниях материальной точки при отсутствии силы сопротивления, можно довести решение до результата в обнтем виде и затем подставить в него численные данные. Рептя же задачу о свободных колебаниях материальной точки при наличии силы сопротивления, надо подставить численные данные в составленное дифференциальное уравнение и определить ,ч и k, так как в зависимости от соотношения коэффициентов п и k приходится записывать решение уравнения в тригонометрических либо в гиперболических функциях (случаи малого, большого сопротивлений и предельный случай). Задача 244. Груз веса Я=98 г подвешен к концу пружины, находившейся в начальный комент в покое в иедеформированном состоянии, и отпущен без толчка. Найти уравнение колебаний груза, если известно, что для деформации пружины иа 1 см надо приложить к ней силу, модуль которой равен 14,4 г. 1 ... 4 5 6 7 8 9 10 ... 66 |
||||||||||
 |
 |