Промышленное охлаждение - freezart.ru. Схемы и периодика

Главная » Мануалы

1 ... 3 4 5 6 7 8 9 ... 51

К задаче 1.20.

приложенная в точке А. Момент присоединенной пары т„ равен m p=-Va.

Следовательно, помимо силы V, приложенной в точке А, мы имеем две пары сил с моментами OTq и /и„р. Эти две пары сил эквивалентны равнодействующей паре сил с моментом /Ид, равным /гад=/гао--Wnp=4l/a- Уа = ЪУа. Величина /Ид является искомым главным моментом системы сил относительно нового центра приведения А.

Итак, в результате перехода от старого центра приведения О к новому центру А главный момент системы измени.1ся.

2. Эту задачу можно решить, восиоль-зовавщись тем, что сила V, равная главному вектору системы сил, является статическим инвариантом, т. е. не зависит от выбора

центра приведения, а главный момеНт системы изменяется. Как известно, главный момент произвольной плоской системы сил относительно нового центра приведения равен алгебраической сумме главного момента этой системы относительно старого центра и момента относительно нового центра главного вектора системы, приложенного в старом центре, т.е. /Ид = = /Ид -- /Ид (о)- Учитывая, что но условию /Ио=41/а, а /Ид (о) = - -Va, находим mJ=ЪVa.

Задача 1.21. К диску приложены четыре силы: Fi = F<i = F, F3 = Fyr, Fi = FV6.

Привести эту систему сил к простейшему виду.

Решение. Взяв начало координат в центре О диска, направим ось X по горизонтали направо, а ось у по вертикали

вверх. За центр приведения системы примем точку О. Определим главный вектор V и главный момент /Ид данной системы сил. Так как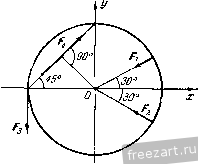

К задаче 1.21.

TO предварительно вычислим проекции н Vy глав.чого вектора V

на декартовые оси координат и сумму моментов /Ид (f,) всех спл

относительно точки О:

Vx=Fkx= - Fl cos 30° - Fi cos 30° -f F cos 45°, (2)

VyI. Fky = - 1 cos 60° -f F-i cos 60° - FaFi cos 45°, (3)

2 >По *) = £з - /4 a sin 45°, (4)

где буквой a обозначен радиус диска. Из (2) -(4) получим: V = 0, Vy=0, tnQ{F ) = 0. Теперь формулы (1) принимают вид: V=0, OTo = 0.

Итак, главный вектор V и главный момент /jIq оказались рав-тлмн нулю. Как известно, это условие является необходимым и доста-точЕгым для равновесия твердого тела. Значит, диск иод действием данной системы сил находится в покое.

Задача 1.22. Вдоль сторон равностороннего треугольника направлены три равные но модулю силы f, = F.21 = Fj = Длина стороны треугольника равна а.

Привести систему сил к нростейше.-гу виду.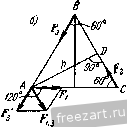

К задаче 1.22.

P e HI e н и е. Выбрав начало осей декартовых координат в вершине треугольника Л, направим ось х но горизонтали направо и ось у по вертикали вверх. Определим главный вектор и главный момент данной плоской системы сил. Выберем в качестве центра приведения точку А.

Модуль главного вектора данш.гх сил вычислим по формуле V=VVi- V?, где

\х = Fkx ==Fi - Fi cos 60° - F3 cos 60° = 0, Vy = Fky = F\ cos 30° - F3 cos 30° = 0.

Следовательно, главный вектор равен нулю: V = 0.

Вычислим главный момент данной системы сил относительно центра приведения А. Учитывая, что

д(Л)==/ л(£з) = 0,

mA{F,) = F.rAD = Fa,

получим: г -

mj, = (F0 + отд (F,) + /Яд (F,) = Fa.

Итак, выбрав в качестве центра приведения данной системы сил точку А, мы нашли:

т. е. установили, что система сил приводится к паре сил с моментом m = XFa. Как известно, в случае приведения системы сил к паре

сил главный момент не зависит от выбора центра приведения.

Эту задачу можно было решить иначе. Так, например, совершив перенос силы F3 по ее линии действия в точку А, можно сложить силы Fi и F3, приложенные в точке А (рис. б). CyMMOii этих сил будет сила F, являющаяся диагональю ромба, угол при вершине которого равен 120°. В этом случае диагональ ромба равна его стороне, т. е. Fi 3 = F. Итак, данная система сил оказалась приведенной к паре сил, в состав которой входят силы F и F, : с плечом

h = AD = aX. Момент этой пары сил равен m = Fh = \Fa.

Второй вариант решения задачи оказался более коротким. Однако следует иметь в виду, что в первом варианте использован более общий прием приведения произвольной плоской системы сил к простейшему виду, которым неизмешю следует пользоваться при решении более сложных задач.

Задача 1.23. Привести к простейшему виду систему сил F F и F3, изображенную на рис. а. Силы Fj и F направлены по противоположным сторонам, а сила Fj - по диагонали прямоугольника

ABCD, сторона AD которого равна а. ) Fj = F = 1з i = F.

Решение. Выбрав начало осей декартовых координат в вершине прямоугольника А, направим ось х по горизонтали направо, а ось у по вертикали вверх. (Выбор таких направлений осей х и j; удобен, так как две силы из трех параллельны осп у и не дают проекций на ось дг.)

Приведем данную систему сил к главному вектору н главному моменту. Выберем в качестве центра приведения системы сил начало координат А. Найдем сначала проекции главного вектора на оси координат:

V.. = S Fft = - Fa cos 30° = - F УГ, = S F,y = Fi 4- F, - Fa cos 60° = F. Модуль главного вектора V равен

V=VviTv! = 2F, (1)

а направляющие косинусы будут:

cos (х, V)

cos (;/>) = = ,

т. е. (х, V) = 150°, (у, V) = 60°. Сила V изображена на рис. б.

Переходим к определению главного момента системы сил относительно центра приведения А. Учитывая, что

(Fi) = Отд (з) = 0, а отд (/= <.) = Fi-AD = Fa,

находим:

= А (i) -f fA (Р-г) 4- (£з) = Fa. (2)

Итак, система сил оказалась приведенной к силе V и паре сил с моментом /Ид, направленным против часовой стрелки.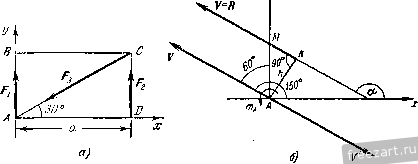

К задаче 1.23.

Известно, что если V 0 и Отд f: О, то систему сил мож1Ю привести к равнодействующей силе /?. Для этого изобразим пару сил, соответствующую главному моменту /Ид, так, чтобы силы, входящие в состав пары сил, равнялись по модулю силе V, причем одна из них (У) лежала бы на одной линии действия с силой V и была направлена ей противоположно. При этом вторая сила, входящая в состав пары сил, приложенная в точке К, окажется векторно равной силе V. Плечо пары h = АК следует подобрать так, чтобы момент этой нары сил был равен главному моменту Отд, т. е. /Яд= Vh, откуда h = = АК= nijjV. Воспользовавшись формулами (1) и (2), находим /2 = а/2. Теперь мы получили систему, состоящую из трех сил. Модуль каждой из этих сил равен модулю главного вектора V. Две силы, приложенные в точке А, равные по модулю и направленные в противоположные стороны по общей линии действия, уравновешиваются. Эти силы можно отбросить, не нарушая состояния твердого тела. Остается одна сила V, приложенная в точке К, эквивалентная

данной системе сил. Следовательно, эта сила, равная главному вектору V, является равнодействующей /?. Таким образом, нам удалось привести данную систему сил к равнодействующей R.

Определим уравнение линии действия равнодействующей /?, воспользовавшись уравнением

xRy-yRx=jmj,{F,). (3)

Проекции равнодейсввующей /? на оси декартовых координат равны проекциям главного вектора V на соответствующие оси, т. е. =

= - , Ry = F. Сумма моментов всех данных сил относительно начала координат А является главным моментом /Лд, определяемым формулой (2):

2/Ид =/Ид = Fa.

Подставив значения R, R S л (л) в уравнение (3), находим уравнение линии действия равнодействующей R:

Это - уравнеште прямой с угловым коэффициентом, равным -]/з/3, откуда следует, что угол, образованный этой прямой с осью х, составляет 150°.

Найдем точки пересечения линии действия равнодействующей с осями координат. Имеем: при х=0 v = -5-а, при у = 0 х = а.

Следовагельпо, равнодействующая направлена по диагонали DB прямоугольника ABCD.

§ 3. Равновесие системы твердых тел

В статике твердого тела наряду с равновесием одного тела рассматриваются сочлененные системы материальных тел, т. е. совокупности твердых тел, касающи;<ся друг друга своими поверхностями или соединенных друг с другом шарнирами, гибкими нитями или стержнями.

Важной задачей статики системы твердых тел является определение реакций связей. Для этого основным является способ расчленения, при котором наряду с равновесием . всей системы тел рассматривается равновесие отдельных тел (или rpyim тел системы). При этом все остальные тела системы и соответствующие связи мысленно отбрасываются, а их действие на тело, равновесие которого рассматривается, заменяется реакциями.

Следует заметить, что при рассмотрении равновесия всей системы твердых тел реакции связей между телами, входящими в систему, не

Рис. 1.33.

должны учитываться; они не входят в уравнения равновесия, как внутренние, взаимно уравновешенные силы. А при рассмотрении равновесия каждого тела в отдельности или какой-либо группы тел, входящих в систему, соответствующие реакции связей, которые были мысленно расчленены, становятся внешними силами и входят в уравнения равновесия.

Задачи на равновесие системы твердых тел, находящихся под действием произвольной плоской системы сил, решаются путем применения уравнений равновесия твердого тела, разобранных в § 2 (уравнения (1*) или (2*), или (3*)).

Рассмотрим в качестве примера системы твердых тел, изображенные на рис. 1.33, 1.34.

1Иатунно-кривошипный механизи ОАВ (рис. 1.33) состоит из трех твердых тел: кривошипа OA, шатуна АВ и ползуна В. Эти тела соединены друг с другом шарнирами А w В. Кроме того, на них наложены еще две связи: шарнирное закрепление в точке О и горизонтальные направляющие, препятствующие вертикальному перемещению ползуна В.

Цилиндрический стакан (рис. 1.34) поставлен вверх дном на горизонтальный пол, внутри стакана покоятся два шара. Эта система состоит из трех твердых тел: шара О uiapa 0-2 и стакана, находящихся друг с другом в контакте. На эту систему тел наложена одна внешняя связь: гладкий горизонтальный пол.

При решении задач на равновесие системы тел недостаточно, как правило, рассмотреть равновесие этой системы в целом. Для всей системы условия равновесия сводятся или к трем уравнениям равновесия для плоской системы сил, или к двум уравнениям для плоской системы параллельных сил. В этом случае число неизвестных может быть больше числа перечисленных уравнений.

Однако это обстоятельство еще не делает систему статически неопределимой, так как если разделить систему на отдельные твердые тела и составить уравнения равновесия для каждого из них, то число новых неизвестных может быть меньше числа новых уравнений равновесия. Если число всех составленных таким образом независимых уравненнй равновесия для всей системы и отдельных ее частей будет равно числу всех неизвестных, то такая задача является статически определенной.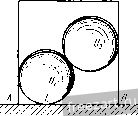

Рис. 1.34.

Поясним это на примере трехшарпирной арки (рис. 1.35, а). Лрка состоит из двух симметричных нолуарок, соединенных в точке С шарниром. В точках Л и Д арка шарнирно прикреплена к фундаменту.

Иа арку действуют две активные известные силы: горизонтальная сила Q, приложенная в точке D. и вертикальная сила Р, приложенная в точке Е. Применяя принцип освобождаемостн от связей, отбросим мысленно шаршфиыс закрепления в точках Л и Б и заменим их действие силами реакций. Величины и направление эжх реакций неизвестны. Следовательно, их можно предс1ави1ь двумя составляю-Ах Рл\ Рцх Таким образо.м, для системы

щиын каждую: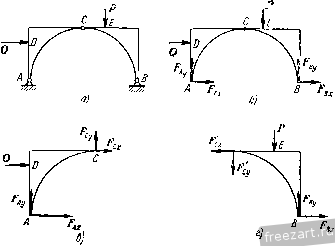

Рис 1 33.

тьердых тел, сосюяшей из двух нолуарок (рис. 1.35, б), можно cocia-вшь три уравнения равновесия, в то время как число неизвестных сил равно четырем. 1ем не менее задача является статически определенной. Рассмотрим равновесие какоМ-.Н1бо одной нолуарки (рис. 1.35, в). На левую но;1уарку деИс1вус1 одна сила Q. Отбрасывая мысленно шарниры Л и С вмес1е с правей нолуаркой, заменяем их действие реакциями, [еакция в точке А представлена двумя ранее выбранными составляюишми Fj и реакция в точке С, также

неизвестная но величине н но направлению, определена составляющими Fx и Fy. Для левой нолуарки можно составить три уравнения равновесия, между тем как новых неизвестных только два; F. и F(.y. Таким образом, рассматривая равновесие всей арки и левой нолуарки, имеем шесть уравнеик.Н равновесия и шесть неизвестных, т. е. задача является статически определенной. Эта же задача может

3 М и Бать н др , т. 1

быть решена и другим способом, если рассмотреть равновесие левой полуарки (рис. 1.35, в) и отдельно равновесие правой полуарки (рис. 1.35, г) И в этом случае число уравнений равновесия равно числу неизвестных (шести). На основании пятого закона (закон равенства действия и противодействия) составляющие Fcx, Р'су реакции шарнира С, приложенные к правой полуарке, равны по модулю и направлены прямо противоположно соответствующим составляющим реакции того же шарнира С, приложенным к левой нолуарке.

При решении задач на равновесие твердых тел надо выполнить четыре первых пункта указанных в начале книги, на стр. 15. При этом следует выделить систему твердых тел и отдельные твердые тела, входящие в систему, равновесие которых надо рассмотреть. Затем:

5) сопоставить число неизвестных величин и число независимых уравнений равновесия; эти числа должны быть равны, если задача является статически определенной;

6) выбрать наиболее удобные системы координат; при этом для каждого тела и для всей системы тел может быть избрана своя система координат;

7) составить уравнения равновесия для каждого твердого тела или для каждой системы твердых тел, равновесие которых исследуется;

8) решить систему всех уравнений равновесия.

Если система твердых тел разделяется на отдельные тела, то при замене их взаимодействия реакциями связей следует ввести реакции, приложенные к одному телу, и на основании закона равенства действия и противодействия выбрать реакции, действующие на второе тело, равными по модулю и направленными прямо противоположно (см., например, рис. 1.35, в и рис. 1.35, г).

В том случае, когда значение неизвестной силы окажется по ответу отрицательным, направление этой силы следует взять противоположным тому, которое было изображено на рисунке.

При составлении уравнений равновесия целесообразно оси координат и точки, относительно которых составляются уравнения моментов сил, выбирать так, чтсбы в каждое уравнение входила только одна неизвестная величина.

Если по условию задачи требуется определить лишь некоторые неизвестные величины, то надо составить только те из уравнений равновесия, которые необходимы для получения ответа.

Задача 1.24. Два гладких цилиндра А w В помещены в ящик (рис. а). Цилиндр А весит Q = 40 кГ и его радиус R = 80 мм; цилиндр В весит Р = 30 кГ и его радиус г = 50 мм.

Определить реакции вертикальных стен в точках С и f, горизонтального иола в точке D и давление между цилиндрами, если ширина яишка 250 мм.

Решение. Отбросим мысленно стены и пол ящика и рассмотрим равновесие каждого цилиндра в отдельности. Цилиндр В находится в равновесии под действием трех сил: веса Р, горизонтальной реакции стены F и реакции N цилиндра А, направленной но прямой, соединяющей центры О и Oi обоих цилиндров (рис. б).

Чтобы найти угол а, образованный реакцией N с горизонтом, рассмотрим треугольник OOiH (рис. в). В этом треугольнике сторона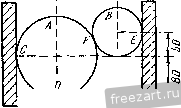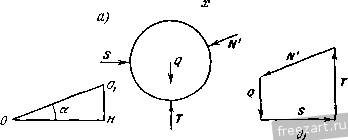

К зацаче 1.24.

00, =/?4-= 30 ММ, катет 0H=\2Q мм. Пользуясь теоремой Пифагора, находим длину второго катета О,/У =50 мм. Таким образом,

5 12

sina=-j-3-,

cosa=.i3.

Составим уравнення равновесия для цилиндра В. Так как линии действия сил, приложенных к цилиндру, пересекаются в центре цилиндра, то достаточно составить два уравнения, приравняв нулю сумму проекций всех сил на оси х я у (рис. а):

F,y=Ni- Q,2cos30°

Из !!ервого урав!!е!1ия найдем:

7-.2 = Q sin 30°= 300 кГ.

Подставляя значение Р=30 кГ, находим:

Л/ = 78 кГ, F = 12 кГ.

Цилиндр А находится в равновесии под действием четырех сил: веса Q, горизонтальной реакции стены S, вертикальной реакции пола Т и реакции N цилиндра В, равной по величине и направленной противоположно силе N. Все четыре силы (рис. г) пересекаются в точке О, центре цилиндра А. Составим два уравнения равновесия этих сил. Суммы проекций сил на ось х и ось у равны нулю:

S := Г - Q - Л/ s i n а = 0.

Отсюда находим:

5=72 кГ, 7=70 кГ.

Следует заметить, что эта задача может быть решена и другим, графическим способом. Действительно, зная величину и направление силы Р, а также направления сил N F, строим силовой замкнутый треугольник. Этот треугольник совпадает с треугольником OOiH (рис. в), если сторону 0/У положить равной силе Р. Тогда сторона ON даст в этом же масштабе силу F, а сторона OOj силу N.

Далее строим замкнутый силовой многоугольник для сил, прило-женныхк цилиндру А. Построение начинаем с известных по величине и направлению сил N и Q. Проводя из конца силы Q прямую, параллельную S, а из начала сил!.! Л^ прямую, параллельную Т, получаем замкнутый силовой многоуголы!ик (рис. д), стороны которого в избранном масштабе и определяют hciisrcctui.ic силы.

Задача 1.25. Блоки Лий весом соответственно 600 кГ и 300 кГ удерживаются и равновесии на гладкой !1лоскости, 1!акло1:ен1!ой !1од углом 30° к горизонту, силой Р, параллельной 00, при !1омощи рычага ОД перпендикулярного к на!{ло!11!ой плоскости (рис. а). Тросы, соединяющие рычаг с блоками, также нараллель!1Ы !1лоскости OOj.

Определить, пре!!ебрегая трением, усилия в тросах и величину СИЛЫ Р. Расстоя1!ия 0Я=8 см, НС=8 см, CD= 16 си.

Р е ш е !1 и е. Рассмотрим равновесие каждого блока в отдельности и равновесие рычага. Блок А (рис. б) находится в равновесии под действием четырех сил: веса Q. !1атяжения T.i, параллельного наклонной плоскости, реакции V, блока В и реакции наклонной плоскости N. перпендикулярных к плоскости 00,.

Выберем оси координат ху (рис. а) и составим урав1!е!!ия равновесия:

i:/-*.= 7-.a-Q,aSin30° = L, ,

1 ... 3 4 5 6 7 8 9 ... 51