Промышленное охлаждение - freezart.ru. Схемы и периодика

Главная » Мануалы

1 2 3 4 5 6 7 8 ... 51

К составлению уравнений равновесия. Составим уравнение проекций на вертикальную ось у и уравнение моментов относительно точки D:

Из первого уравнения находим /?д = Р--F = 2000 я, а из второго получим /Ир = 3800 дж. Положительные значения Rjj и указывают, что направления силы и реактивной пары с моментом /Ир были выбраны правильно.

Рекомендуем решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, издания 1950 г. и последующих лет: 78, 87, 89, 90.

Переходим к решению задач на равновесие твердого тела, к которому приложена произвольная плоская система сил. При решении этих задач надо выполнить четыре первых пункта, указанных в начале книги па стр. 15. Затем:

5) убедиться в том, что данная задача является статически определенной, т. е. что число неизвестных неличин не более трех;

6) выбрать направлення осей декартовых координат и точку (или точки), относительно которой предполагается составить уравнение моментов;

7) составить уравнения равновесия твердого тела;

8) решить систему нолуче1И1ых уравнений равновесия и определить неизвестные величины.

Уравнения равновесия можно составить в любом возмож1юм виде (см. выше, стр. 44, формулы (1*), (2*), (3*)).

Следует стремиться к получещш таких уравнений равновесия, в каждое из которых входила бы только одна неизвестная величина. В этом случае можно каждую из неизвестных величин непосредственно определить из соответствующего уравнення. Для этого оси координат целесообразно направить так, чтобы некоторые неизвестные силы оказались перпендикулярными к этим осям. Тогда величи1н>1 этих неизвестных сил-в соответствующее уравнение проекций не войдут. Центр моментов, т. е. точку, относительно которой должно быть составлено уравнение моментов, следует выбрать в точке пересечения линий действия двух неизвестных сил. Это дает возможность непосредственно определить из соответствующего уравнения моментов величину третьей неизвестной силы. Если, однако, этот центр моментов расположен так, что вычисление плеч при определении моментов сил представляет значительные трудности, то лучше составить относительно другого центра такое уравнение .моментов, в которое войдут величины

днух неизвестных сил, и затем совместно решить полученную систему уравнений.

Если направление какой-либо реакции связи неизвестно, то следует заменить ее двумя составляющими, направив их параллельно осям кг ординат в сторону положительного отсчета. Если в результате решения знак величины какой-либо силы окажется отрицательным, то это означает, что направление силы противоположно тому, которое было предварительно указано на рисунке.

В тех случаях, когда по условию задачи требуется определить давления твердого тела на оггоры, нужно найти равные по модулю этим давлениям соответствующие реакции связей, а затем направить иско.мые давлег1ия противоположно этим реакциям.

Задача 1.15, Горизонтальная однородная балка/4fi длиной/= 4 .и и весом Р=1 Г, прикрепленная шарниром А к стене, удерживается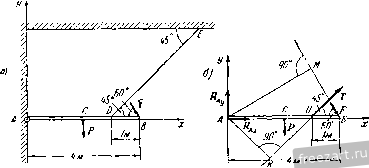

К задаче 1.15.

в ран1говесии тросом DE, расположенным под углом 45° к горизонту, DB=l м. К свободному концу балки приложена сосредоточенная сила F = 2T, образующая угол 60° с горизонтом.

Определить давление балки на шарнир А и натяжение троса DE.

Решение. Рассмотрим равновесие балки АВ, на которую действуют две активные силы: вес балки Р, приложенный в ее середине (АС=СВ=2м), и сосредоточенная сила F, приложенная в конце балки В.

На балку наложены две связи, шарнир А и трос DE. Мысленно оборвав трос DE, заменяем действие троса на балку реакцией троса Т, направленной от точки D в сторону обрыва. Направление реакции шарнира А заранее указать нельзя. Поэтому изобразим две взаимно перпендикулярные составляющие этой реакции. Направим ось л: вдоль оси балки по горизонтали направо, а ось у по вертикали вверх. Составляющие реакции и Rjy направим вдоль осей координат в сторону их возрастания.

Так как

АК АК-

АСЧм, ЛАГ = Л1) sin 45° = у 1/2 AM = Л5 sin 60° = 2 Уз м,

7==1-}-241/6=(1-}- 21/3) = 4,2 Т.

Подставив это значение Т в уравнения (1) и (2), получим: Rx = - 3,96 Т, Rjiy = - 0,23 Т.

Знак минус, стоящий в выражении /?д^, указывает, что наиравле-I иг составляющей реакции шарнира Rj противоположно тому, которое было указано на рис. б, т. е. сила Rj направлена по горизонтали налево; аналогично сила 4 направлена по вертикали вниз.

Искомые давления балки на связи направлены противоположно соответствующим реакциям связей и равны им по модулю, т. е. горизонтальная составляющая силы, действующей на щарнир, равна 3,96 7 и направлена по горизонтали направо, вертикальная составля- . ющая силы, действующей на шарнир, равна 0,23 Т и направлена вверх, натяжение троса равно по модулю 4,2 Т.

Задача 1.16. Иа рис. а изображена симметричная стропильная ферма длиной 1=10 м, весом Р=12 7, стоящая на двух опорах, причем левая опора А расположена на катках, которые могут перемещаться вдоль горизонтальной плоскости. Перпендикулярно к АЕ в точке D, на расстояшш AD=2 м, приложена сосредоточенная сила F=AT, £ЕАВ = гО°.

Теперь балку можно рассматривать как свободное твердое тело, находящееся в равновесии под действием пяти сил, причем лищь величины трех сил Т, Rjix и j, неизвестны. Следовательно, задача является статически определенной.

Составим уравнения равновесия балки в проекциях на оси х и у и уравнение моментов относительно точки А. Выбор точки А в качестве центра моментов удобен, так как моменты двух неизвестных по величине сил Rj и Рау относительно точки А равны нулю и в уравнение моментов войдет лищь одна неизвестная Т. Уравнения равновесия имеют вид

2 = /?д^ + 7 cos 45° + F cos 60° = 0, (i)

2 Ffcj, = Rjy - P-]-T cos 45° - F cos 30° = 0, (2)

m;{F)=T-AK - P-AC-F-AM = Q. (3)

Из уравнения (3) находим

Определить опорные реакции в точках Л и S. Решение. Рассмотрим равновесие фермы, к которой приложены две активные силы: вес фермы Р и сосредоточенная сила F.

Так как катки не препятствуют перемещению фермы в горизонтальном направлении, то опорная реакция Rj направлена перпендикулярно к горизонтальной плоскости. Указать заранее направления опорной реакции в точке В невозможно. Поэтому в опоре В следует

изобразить две взаимно перпендикулярные составляющие реакции (рис. б).

Направим ось х по горизонтали направо, ось у по вертикали вверх, а составляющие реакции пх И liiy параллельно соответствующим координатным осям.

Итак, к ферме приложены пять сил, в том числе три неизвестные по модулю силы: Rj, R и ду. Следовательно, за-I дача является статически определенной.

Используем уравнения равновесия фермы в проекциях на оси х ч у и уравнение моментов относительно точки А. Составление уравнений проекций на оси л: и у целесообразно потому, что силы Rj и Rgy перпендикулярны к оси х, а сила Rijx перпендикулярна к оси у. Следовательно, эти три неизвестные по модулю силы в соответствующие уравнения проекций не войдут. Выбор точки А в качестве центра моментов удобен потому, что линии действия сил Rj и пересекаются в этой точке. Следовательно, моменты этих сил относительно точки А равны нулю и в уравнение моментов войдет лишь неизвестная величина силы Уравнения равновесия имеют вид

E/*. = /cos60° + Rb, = 0. (1)

F,y = R-{-Ry-F cos Ж-Р = 0, (2)

mj,iF,) = -F-AD-P-AK-RByAB = 0. (3)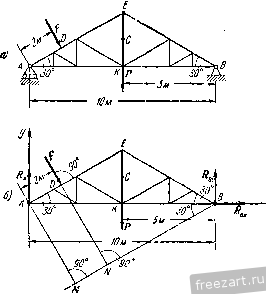

К задаче 1.16.

Из уравнения (3) находим:

Учитывая, что AD - 2m, АК=Ь м, AB=\Q м, F=4 Т, Р=П Т, получаем, что /?д^, = 6,8 Т. Подставив это значение Ry в уравнение (2), имеем Д;д=8,66 Т. Из уравнения (1) находим, что Яцх = = -Fcos 60°= -2 7.

Знак минус, полученный в выражении для Rg, указывает, что направление составляющей опорной реакции противоположно

тому, которое было указано на рисунке, т. е. сила Rg направлена по горизонтали налево.

При рещении системы уравнений (1), (2) и (3) модули неизвестных сил Rgx и Rgy были непосредственно определены из уравнений (1) и (3). /1ищь величину силы Rj пришлось вычислить из уравнения (2), подставив в него значение Rgy. Однако можно составить такую систему уравнений равновесия, чтобы из каждого уравнения была, независимо от других, определена каждая из неизвестных. Действительно, сохранив уравнения (1) и (3), составим вместо уравнения (2) такое уравнение моментов, чтобы в него вошла лишь одна неизвес!-ная R. Для этого необходимо, чтобы моменты двух друтих неизвестных сил, т. е. Rgx и Pbv> оказа;и1сь равными нулю. Этому условию легко удовлетворить, выбрав за центр моментов точку пересечения линий действия этих сил, т. е. точку В. Итак, вместо уравнения (2) составим уравнение моментов сил относительно точки В:

mg(F,) = ~R.AB-\-P.KBF.NB = 0. (4)

Из уравнения (4) непосредственно находим:

А - Р-АВ--АВ-

Учитывая, что КВ = Ъ м, ЛД=10 м, NB = MB - MN= АВ со%ЪО° ~ ЛО = 5Уз - 2 = 6,65 л, Р=12 7, F=4 7, получим йд = 8,66 Т.

Задача 1.17. Ознакомившись с условием и решением задачи 1.G, определить силы Rj к F с учетом веса суппорта, приложенного в его центре тяжести С и равного Р = 60 кГ.

Решение. В задаче 1.6 мы рассмотрели равновесие суппорта под действием трех сил: N, F а Rj, использовав теорему о трех непараллельных силах. Теперь к этим силам добавляется вес суппорта Р. Это лишает нас возможности применить теорему о трех непараллельных силах, с помощью которой мы смогли определить положение линии действия реакции Rj цилиндрического щар1гира А. Поэтому заменим силу /?д двумя взаимно перпендикулярными состав-ляюишмн. Направив ось х но горизонтали направо, а ось у по вертикали вверх, изобразим на рис, б составляющие Ri и Rjy.

Итак, суппорт находится в равновесии под действием плоской системы пяти сил; Л^, Р, F, R fAy Задача является статически определенной, ибо число алгебраических неизвестных равно трем: F, Rax и R-Ay

Составим уравнения проекций ira оси х п у н уравнение моментов относительно точки В. Выбор точки В целесообразен, ибо линии

действия двух неизвестных сил R и F пересекаются в точке В. Значит, моменты этих сил относительно точки В равны нулю. В уравнение моментов войдет лишь одна неизвестная величина Rjy, которую непосредственно можно будет определить. Уравнения равновесия имеют вид

2*.= -Л/со5бО°+/?д,= 0, (I)

2; Fky = Rav - я - Л' cos 30° +

+ £=0, (2)

2 в (*) P-BC-RjyAB +

-\-N-BS=0. (3)

Из уравнения (3) получим;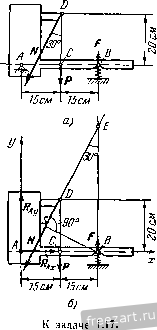

RAy -

P-BC + N-BS АВ

По условию; Р=60л:Г, Л/= 300 кГ, ВС= 15 см, АВ = 30 см. Из треугольника ЛбЯ имеем BSz= BE-sin 30° =

= 46.у=23 см (здесь использована

формула (1) задачи 1.6). Подставив эти значения в (4), находим:

/?д, = 260 кГ. (5)

Затем из уравнений (1) и (2) имеем /? ,==7Vcos 60° = 300-= 150 кГ,

F = Р + Л/ cos 30° - RJy = 60 + 150 ]/3 - 260 = 60 кГ. Итак,

Rjx =150 кГ, Р = 60 к Г. (6)

Использовав результаты (5) и (6), вычислим модуль реакции /?д цилиндрического шарнира А по формуле

Получим:

Ra=Vrax+rXv.

/?д = 300 кГ.

Как и следовало ожидать, учет силы тяжести Р суппорта сказался па увеличении реакции /? и силы упругости F. Нагюмни.м, что при решении задачи 1.G без учета веса cyiniopra эти силь; были но модулю равны: /?д = 275 кГ, Г = 30кГ(см. формулу (3) задачи 1.6).

Как и в предыдущей задаче, вместо уравнения (2) можно составить уравнение моментов относительно точки А. Это дало бы нам возможность сразу определить силу F.

Конечно, задачу 1.6 можно также решить с помощью системы уравнений (1), (2), (3). Действительно, приняв в этих уравнениях />=0, мы получим: Ra= 150 кГ, /?д^, = 230 кГ, F=SO кГ и,

следовательно, = У йж-г j =

Рекомендуем решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, издания 1950 г. и последующих лет: 122, 123, 129, 133, 134, 135, 136, 140.

2°. Опрокидывание твердых тел. При исследовании покоя твердого тела (конструкций) встречаются задачи, в которых следует определить предельные значения сил или размеров, обеспечивающих сохранение этого состояния. В этих задачах обьнпю при величине силы, превышающей наибольшее допустимое значение, обеспечивающее покой твердого тела, происходит опрокидывание тела вокруг одной из точек опоры.

Такие задачи решаются в предположении, что твердое тело начинает отрываться от одной из опор. Поэтому реакции этой опоры не следует учитывать. Тогда при равновесии твердого тела реакция оставшейся опоры должна уравновешиваться с равнодействующей всех активных сил. Это значит, что Л1ИН1Я действия равнодействующей всех активных сил проходит через оставшуюся опору и, следовательно, момент равнодействующей относительно точки опоры равен нулю. Таким образом, в соответствии с теоремой Вариньона сумма моментов всех активных сил относительно точки опоры О равна нулю:

iio (F )=o.

Из этого уравнения определяются предельные значения сил или размеров твердого тела, при которых еще не наступает опрокидывание.

Решение задач на опрокидывание твердых тел надо проводить в следующем порядке:

1) изобразить активные силы;

2) определить опору, относительно которой может произойти опрокидывание твердого тела;

3) составить уравнение моментов активных сил относительно этой точки опоры;

4) решив уравнение, определить искомую величину (предельную силу или предельный размер).

Задача Ы8. Горизонтальная консольная балка АС весом Р лежит на опорах А и В, причем опора А расположена на катках, не препятствующих перемещению вверх. К консольному концу С

К задаче 1.18.

балки приложена сосредоточенная вертикальная сила F.

Определить наибольи1ее значение силы F, при котором балка остается в покое. Размеры указаны на рисунке.

Решение. На балку действуют две активные силы: вес балки Р, приложенный в середине балки, т. е. на расстоянии 1 м от опоры В-, F-сосредоточенная сила, приложенная в конце консоли, т. о. в точке С.

Нетрудно видеть, что при большом значении силы F произойдет опрокидывание балки вокруг опоры В в направлении по часовой стрелке.

Для определения наибольшего значения силы F надо сумму моментов активных сил относительно точки В приравнять нулю:

ms(F,) = p.l-F-2 = 0,

Р Р

откуда F = -. Если сила F-j, то происходит опрокидывание балки вокруг опоры В в направлении по часовой стрелке.

Задача 1.19. Подъемный кран установлен на грузовой автомашине. Вес противовеса В равен P<j = 2 Т. Вес автомашины с краном без

противовеса, равный Pj = 5 7, приложен в точке С.

Определить наименьшее расстояние DE между осями колес автомашины и наибольший вес Pj поднимаемого груза А, при наличии которых автомашина не опрокинется как с грузом А, так и без него. Размеры указаны на рисунке.

Решение. К грузовой автомашине с установленным на ней подъемным краном приложены активные силы: Р, - вес автомашигн ! с краном без противовеса В, Р^ - пес противовеса В. При наличии груза А приложен также его вес Pj.

При подвенгенном грузе А может произойти опрокидывание автомашины в направлении против часовой стрелки вокруг точки касания D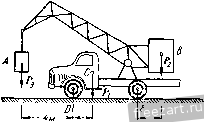

t,5u 2м

К задаче 1.19.

переднего колеса с землей. При отсутствии груза А может совер-пгнться опрокидывание автомашины под действием противовеса В в направлении по часовой стрелке вокруг точки касания Е заднего колеса с землей. Иные варианты опрокидывания не рассматриваем как практически неинтересные.

Для определения наибольшей величины веса поднимаемого груза А и наименьшего расстояния DE между осями колес, обеспечивающего равновесие автомашины, надо составить: 1) уравнение моментов активных сил относительно точки D с учетом момента веса /*, 2) уравнение моментов активных сил относительно точки Е без учета момента веса Р^. Эти уравнения имеют вид

Рз-4 -Pi-1,5 - P.j(D£ + 2) = 0, Р, (DE~ 1,5) -P.j.2 = 0.

Реншв эту систему уравнений равновесия при Р., = 5 Т, Р^=2 Т, находим: Рз = 4 Т, БЕ=2,Ъ м. Таковы предельные значения Р^ и DE, обеспечивающие равновесие автомашины.

В случае Рз>4 Г произойдет опрокидывание автомашины вокруг точки D в направлении против часовой стрелки.

В случае DE<2,3 м при отсутствии груза А произойдет опрокидывание автомашины вокруг точки Е в направлении но часовой стрелке.

Рекомендуем решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, издания 1950 г. и последующих лет: 94, 95, 96.

3°. Приведение произвольной плоской системы сил к простейше.му виду. Рекомендуется следующий порядок выполнения приведения:

1) выбрать оси декартовых координаг,

2) выбрать центр приведения систе.мы сил;

3) вычислить проекции главного вектора системы сил по формулам

k=l Л=1

4) определить модуль главного вектора V=l/V-j-и направ-ляюитие косинусы

cos (jCv) = cos (/V) = ;

5) вычислить главный момент системы сил относительно центра приведения по формуле

где О - центр приведения системы сил;

6) в зависимости от значений V и /Ид возможны четыре случая:

а) если V О и iiIq ф О, то следует систему привести к равио-действуюи1ей R, равггой силе V, отстоящей от нее на расстоянии h = mQlV и расиоложснной так, чтобы знак момента равнодействующей относительно центра О совпадал со знаком главного момента

б) если УфО, mQ = 0, то система сил приводится к равнодействующей, совпадающей с V;

в) если V = 0, MqQ, то система сил приводится к паре сил с моментом OTqI

г) если V=0 и /Яо = 0, то система сил находится в равновесии. Уравнение линии действия равнодействующей в случаях а) и 6)

имеет вид

к = 1

где Rx=Vx, R=Vy, а х и j/ -текущие координаты точки линии действия равнодействующей, О - начало координат.

Оси декартовых координат следует направлять так, чтобы силы в возможно большем числе оказались параллельными либо перпендикулярными к этим осям. Центр приведения системы следует выбирать так, чтобы моменты сил относительно этого центра в возможно большем числе обратились в нуль, т. е. чтобы линии действия этих сил проходили бы через центр приведения системы.

При переходе от одного центра приведения (О) к другому центру приведения (А) следует иметь в виду, что главный вектор V от выбора центра приведения не зависит (главный вектор является статическим инвариантом), а главный момент системы изменяется в соответствии с формулой

Задача 1.20. Произвольная плоская система сил была приведена к центру О. В результате приведения были получены сила V (см. рисунок) и пара сил, момент которой равен главному моменту mQ = 4Va.

Определить главный .момент этой системы сил при переходе к FFOBOMy центру приведения А, находящемуся на расстоянии ОА = а от старого центра по оси х.

Решение. Выбираем Оси декартовых координат так, как это изображено на рисушсе.

Задачу можно реншть двумя способами.

1. Приведем силу V к точке А. Для этого приложим в точке А две уравновешивающиеся силы V и V так, чтобы одна из них была векторно равна силе V. Теперь сила V оказалась ггриведенной к точке А. При этом добавилась пара сил (присоединенная пара), в состав которой входят сила V, приложенная в точке О, и сила V,

1 2 3 4 5 6 7 8 ... 51