

 |
 |
|
Навигация
|
Главная » Мануалы Блок в (рис. в) находится в равновесии мод действием трех сил: веса Q, реакции /V перпендикулярной к плоскости 00 и натяжения троса Ту, параллельного 00,. Составим уравнения равновесия: F*.= 7-,-Q, sin30° = a Р^У = Л/i - Q, cos 30° = 0. Отсюда находим: Ti = Qi sin 30°= 150 кГ, = 1501/3 кГ. Из второго уравнения системы (1) получим: Nq = Q, cos 30° = 300 . /з + 150Кз = 450\3 кГ. Зная натяжение тросов, рассмотрим равновесие рычага (рнс. г), находящегося под действием сил: Р, - Т^, - Ti и реакции шарнира 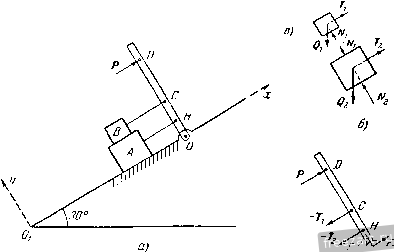 у О К задаче 1.25. О, которую представим в виде ее проекций F оу Уравнения равновесия для рычага будут: >: Ph.. РохЛ-Р- Pi - 7jО, 2:,3,=/03,=О, у; ,п^ (F,;) = 7 j 8 + 16 - Р. 32 = 0. 8-300+ 16.150 Отсюда находим: Р = - = 300 кГ. Задача 1.26. В приборе (рис. а) тела А п В могут скользить по сторонам угла К; одна из сторон вертикальна, а другая образует угол 20° с горизонтом. Наклонная плоскость соприкосновения обоих тел составляет угол 40° с вертикалью. Сжатая пружина давит вниз с силой Я =10 кГ на тело А. Пренебрегая весом тел и предполагая, что все соприкасающиеся поверхности гладкие, найти горизонтальную силу Q, удерживающую систему в равновесии. Penjenne. Отбросим мысленно стороны угла К и рассмотрим отдельно равновесие тела А и тела В. На тело А (рис. б) действуют 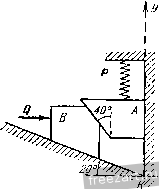  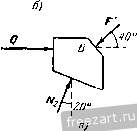 К задаче 1.26. три силы: давление пружины Р, направленное по вертикали вниз, реакция вертикальной стены Л^ направленная по горизонтали влево, и реакция F отброшенного тела В, перпендикулярная к наклонной плоскости соприкосновения обоих тел. Линии действия этих сил пересекаются в одной точке, так как тело А находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости. Следовательно, для них достаточно составить два ураннения равновесия, ириравияв нулю сумму проекций всех сил на оси х а у. Выберем оси так, как это показано на рис. а. Тогда I,F,x = Fcos 40°-Л', = 0, 2F> = Fsin 40° -/5=0. Подставляя значение силы Р, находим из уравнений Я= 15,58 кГ, М = 12 кГ. На тело В (рис. в) действуют три силы: реакция F тела А, равная известной уже силе F, но направленная в соответствии с зако-1ЮМ равенства действия и иротш'-одейстш.л в нротивоноложную сто- рону, неизвестная по величине горизонтальная сила Q и реакция N.. перпендикулярная к наклонной стороне угла, составляющая, следовательно, с вертикалью угол 20°. Запищем для этих трех сил, пересекающихся в одной точке, два уравнения равновесия: ]CF* = Q + M sin 20° -Fcos 40° = 0, 2 Ffc, = Ni cos 20° - F sin 40° = 0. Подставляя в эти уравнения найденное ранее значение F, определяем остальные силы Q = 8,3 kF, Л/=10,6 к Г. Задача 1.27. Двухпролетная Оалка AD (рис. а) с промежуточным щарниром С закреплена шарнирно в точке А. В точках В к D балка опирается при помощи катков на горизонтальные направляющие. А
fcAc К задаче 1.27. Определить реакции опор Л, В, D и усилие в шарнире С, если на балку действуют: пара сил с моме!ггом Л1 = 20 kFm, сила Я = 8 kF, сила Q=12 kF. Даны размеры: АЕ = \ м, ЕВ = 2 м, ВС=Ъ м, CM=MD=2 м. Решение. Система твердых тел состоит из двух балок. Рассмотрим равновесие каждой из балок отдельно. Па балку АС действуют (рис. б): активная сила Р и активная пара сил с моментом М. Кроме того, на балку наложены связи - шарниры А w С, подвижная опора В. Отбрасывая мысленно связи, заменяем их действие реакциями. Так как реакция шарнира А неизвестна по на[[равле!шю и величине, заменяем ее двумя составляющими R и Аггалогично реакция шарнира С также изобразится двумя составляющими Rq и Ry Реакцию опоры В представим вертикальной силой R. Рассмотрим, далее, равновесие балки АС как равновесие свободного твердого тела, находя1це-гося под действием шести сил и 0Д!юй пары сил. Выберем оси координат с началом в точке А, ось абсцисс направим по горизонтали вправо, ось орди![ат по вертикали вверх. Составим уравнения равновесия балки АС: 2:F = /?a.+ /?c.v = 0, (!) mJ{F) = Rg. AB-Y Rcy - AC~ Р АЕ - M = Q. (3) Можно было бы вместо второго уравнения равновесия составить сумму моментов всех сил относительно точки С. В это уравнение вошли бы только две неизвестные силы и И,р так как линии действия остальных неизвестных сил пересекаются в точке С. Однако в обоих случаях уравнение (1) является независимым от остальных уравнений и содержит два неизвестных; уравнения (2) и (3) связаны между собой и содержат три неизвестных. Таким образом, из полученной системы ни одно из неизвестных не может быть определено. Рассмотрим поэтому равновесие второй балки CD (рис. й). На балку действует одна активная сила Q. Прг:-меняя закон освобождаемости от связей, заменим действие шарнира С и опоры D реакциями связей. Реакция направлена по вертикали, иериендикулярно к горизонтальной плоскости, на которую опираются катки. Реакция шарнира С неизвестна по величине и направлению. На основании закона равенства действия и противодействия составляющие этой реакции равны по модулю составляющим реакции шарнира, нриложегшым к балке АС, и направлены в прямо противопо-ложные стороны (рис. в). Таким образом, имеем свобоД!юе твердое тело-балку CD, находящуюся в равновесии под действием пяти сил. Составим уравнения равновесия, выбрав оси координат с началом в точке С; ось абсцисс направим по балке вправо, ось ординат - вертикально вверх. Имеем: y:f-\x--=~Rc. = 0, (4) >] с (Pk) -=RryCD-Q.CHO. (в) В этих трех уравнениях равновесия только одна новая неизвестная If. А всего в шести уравнениях равновесия шесть неизвестных. Из уран-нений (4) и (1) следует: Rc = Rax = 0- Из уравнения (6) находим: Rn=Q-i=2.2/4 = 6 кГ, а из (5) [юлучаем: Ry=R - Q=6-n = - 6 кГ. Знак минус показывает, что в действительности направления составляющих Rq, и Rcy противоположны принятым на рисунке. Далее, из (3) имеем: = Ё AD - О-= S 4/6 Ч- 20/6 -U 6 . 9/6 = 17,66 кГ и, наконец, из (2) находим: R =P~R - R.y = 8-1 7,66 -f 6 = - 3,66 кГ. Знак минус указывает, что и реакция направлена не вверх, как предполагалось, а по вертикали вниз. Задача 1.28. Через блок с неподвижной осью О и радиуса R (рис. а) перекинута нить, к концам которой подвешены два одинаковых груза Pi и Pj. Правый конец 1шти свисает вертикально. Левый конец [шти огибает блок с подвижной осью Oi и радиуса г. Нес блока с подвижной осью g. Ось нижнего блока насажена на конец стержня длиной /, другой конец которого закреплен иа оси верхнего блока. 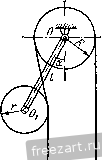 up, Dp, а) 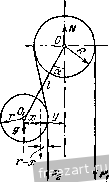 к з,адаче 1.28. 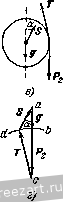 Пренебрегая весом стержня, определить угол я, который образует стержень с вертикалью в положении равновесия, и усилие в стержне 00,. Р, = Р2= 10 кГ, я=4 кГ, R = 4: см, г = Ъ см, /=10 см. Peujenne. Рассмотрим равновесие системы твердых тел, состоя-шей из двух блоков и стержня, соединяющего их центры (рис. б). Для этого мысленно отбросим ось О, поддерживающую верхний блок, и заменим ее реакцией N. Кроме того, на систему действуют внешние силы Я Я.2, g. Реакция N вертикальна, так как все остальные силы заведомо вертикальны. Составим для данной системы параллельных сил два уравнения равновесия: i:Fi = N-Pi-P.,-=0, (F;) = PyR - Р.2 (/ sin а - г) - g-/ sin a = 0. Из первого ураниепия определим реакцию TV: N=P, + Pj + =24 кГ. Из второго уравнения находим угол а: 10.4 - 10(10 sin а-3) - 4- 10 sin а = О, откуда sin а = 1 /2, я = 30°. Для определения усилия в стержне рассмотрим равновесие блока с подвижной осью. Он находится в равновесии под действием четырех сил (рис. в): веса g, двух равных но величине реакций нити и Г, а также реакции стержня S, [гаправленной по стержню, но неизвестной по величине. Таким образом, геометрическая сумма этих четырех сил должна быть равна нулю: P,-T-g-S = 0. Так как угол я известен и Т=Р^, то проще всего величину 5 определить графически, построе!гием силового многоугольника. Отложим из точки а (рис. г) две вертикальные силы и в избранном для сил масштабе. Далее, из точки с, конца силы Р как из центра, проведем дугу окружности радиусом, равным по величине Pj. На этой дуге должен находиться конец силы Т и начало силы S, составляющей уго-л я =30° с вертикалью. Проведя из точки а под углом 30° к вертикали прямую до пересечения с дугой окружности в точке d, соединим прямой точки d и с. Отрезок da и определит величи[)у усилия в стержне. Измерив его в избранном для сил масштабе, находим, 410 усилие в стержне 5=5 кГ. Задача 1.29. Рама состоит из двух жестких частей АС и ВС (рис. а), соединенных шарниром С и прикрепленных к фундаменту шарнирными огюрами Лий. Определить реакции в шарнирах Л, В, С, если в точке D приложена вертикальная сила Р = 1 т. Задачу решить графически. Решение. Реакции шарниров Л и неизвестны т величине и направлению. Следователыю, если рассматривать равновесие всей системы АСВ, отбросив опоры Л и и заменив их действие реашеи-ями, то число неизвестных будет равно четырем, а уравнений равновесия будет три. Рассмотрим поэтому отдельно равновесие левой части рамы (рис. б). К этому твердому телу никаких активных сил не приложено. Применяя закон освобождаемости от связей, отбросим мысленно шарниры Л и С и заменим их действие реакциями. Часть рамы АС находится в рав1Ю-весии под действием двух сил: и R. Согласно второму закону статики эти силы должны быть равны но величине и направлены по одной прямой в разные стороны. Так как одна сила при;[ожена в точке Л, а другая - в точке С, то общей линией действия этих сил будет АС. Рассмотрим, далее, равновесие правой части ВС рамы. К ней приложена одна активная сила Р. Освобождаясь мыслегиго от двух связей: шарниров В и С, заменяем их действие реакциями. Реакция а основании закона равенства действия и противодействия равна по неличине и направлена в противоположную сторону по АС (рис. в). В  А -Rr. -fir -2а~ Л в р 2а к задаче 1.29. Направление реакции может быть определено на основании теоремы о трех непараллельных силах. Действительно, часть НС находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости. Линии действия двух сил известны- 0!Щ пересекаются в точке О. Согласно теореме линия действия третьей силы реакцчп должна также проходить через точку О. Три силы Р, Rc, Rg, линии действия которых пересекаются в точке О, находятся в равновесии. Следовательно, они должны образовать замкнутый треугольник. Откладываем из произвольной точки (рис. г) силу Р, известную по величине и направлению. Из конца силы Р проводим линию, параллельную АС, т. е. линии действия силы Rc. Из начала силы Р проводим линию, параллельную ОБ, т. е. линии действия силы Rj. Получаем замкнутый силовой треугольник, сюроны которого и определяют в принятом для силы Р масштабе величишя искомых реакций: Rc и Rji- Согласно ранее доказаггному реакция шар[[И1)а А равна Rc. Решение задачи об определении реакций шарниров трехшарнир-ной арки осложняется, если среди активных сил, действуюишх на трехшарнирную арку, имеется одна сила, приложенная к шарниру С. Рассмотрим в этом случае трехи]арнирную арку как сос1авленную из трех тел: двух нолуарок и шарнирного болта. Полуарки не соприкасаются друг с другом. Шарнириьгй болт соприкасается с каждой из них. Рассмотрим три возможных варианта задачи. В первом варианте (рис. д) активная сила Р приложена к шарнирному болту, а к [юлуаркам никаких задаваемых сил не приложено. В эюм случае на левую полуарку, находящуюся в равновесии, действуют две равные силы R и R (рис. б), направленные но прямой АС в противоположные стороны. CoBepujenno аналогично па правую полуарку действуют две взаимно уравновешиваюни1еся силы Ro и с,. направленные по прямой ВС. Рассмотрим равновесие шарнирного бол!а С, к которому приложены три силы: сила Р, реакции левой и правой полуарок - R., - Ri (рис. е), причем сила Р известа но величине и направлению, а у реак!щй полуарок известны только ли-[ши действия. Строя замкнутый треугольник (рис. ж), находим вели-Ч1ИГЫ реакций R., R(. и, следовательно, равт.1е им величины /?д, R/j. Во втором вариате (рис. активные силы, кроме шарнирною бол1а С, приложены только к одной правой полуарке (сила Q). Рассмотрим равновесие левой полуарки (рис. б). Направление реакцгй Rc и Rjn совпадает с прямой АС. Далее, присоединяем нгарщфный болт С вместе с ириложегнюй к нему активной силой Р к правой [!олуарке и рассматриваем се равновесие (рис. и) под действием сил: Р, Q, - R(- и реакции R,, г<оторую 1)аскладывае.м па две составлякште R, Rny- Замечая, что -R(- образует угол 43° с горизонталью, составляем три уравнения равновесия: == Rc cos 45° - Q -1- R x = О, у; = Rc sin 49° - P + Ry = 0, Е'л С *) = c 12 - p.a-Q.b = Q, откуда и определяются все три неизвестные. В третьем варианте (рис. к) активные силы приложены, кроме шарнирного болта, и к обеим полуаркам. В этом случае сначала определяем реакции шарниров А и В. Для этого рассмотрим равновесие всей арки, отбросив мысленно шарниры А \л В заме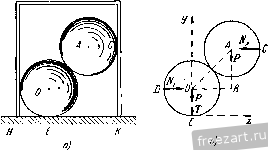
К задаче 1.30. и К. (Ясно, что Ni = Ni и A = Ni.) В момент опрокидывания стакана, который мы рассматриваем, давление в точке Н на пол и, следовательно, реакция пола обращаются в нуль и стакан опирается на горизонтальную плоскость только в точке К. Составим уравнение моментов относительно точки К mK{F,)=.N:-CK-Ni-DH-Q-R = 0. (6) Лалее из (6), учитывая (4), имеем: N-AB - Q-R = 0. Подставляя в это равенство значение N, определегшое формулой (5), имеем: АВ РОВ-АВ ОН Q - N - - ; F,y=T-2P=0. 2 то (Ft)= Ni-AB - P-OB = 0. (1) (2) (3) 1 ... 4 5 6 7 8 9 10 ... 51 |
|||||||||||||||||||||||||||||
 |
 |