

 |
 |
|
Навигация
|
Главная » Мануалы Установим формулу для вычисления алгебраического значения наименьшего главного момента заданной системы сил. Наименьший главный момент системы сил М* равен проекции главного момента рассматриваемой системы сил на направление главного вектора R* (рис. 119): Ж*= MoCOs(Mo. R*). (57.5) Умножив обе части равенства (57.5) на /?*, получим /?*Ж* = /?*МоС08(Л1о, R*). (57.6) Правая часть равенства (57.6) представляет собой величину скалярного произведения R* и Мд, т. е. R*Mo cos (Mq, R*) = R* Mo. (57.7) Выражая скалярное произведение (57.7) через проекции векторов сомножителей на координатные оси, из формулы (57.6) получим /?*. M* = R*-Mo = AM + KMy + ZM. М*=:- -~. (57.8) Формула (57.8) выражает алгебраическое значение наименьшего главного момента М* через проекции R* и Мд на координатные оси. Установим при помощи формулы (57.8) аналитическое условие, при котором пространственная система сил приводится к равнодействующей. Заданную систему сил можно привести к равнодействующей в двух случаях (§ 54): а) если а Л1о==0 и б) если R* # О, }\офО и Мо L R. В обоих случаях М* = Мд cos (IAq, R*) = 0. Поэтому, если система сил приводится к равнодействующей, то выполняются условия: 1) Х^ + У^ + г^фО; (57.9) 2) XMj,-\-YMy-+ZM Соотношения (57.9) являются аналитическими условиями приведения системы сил к равнодействующей силе. § 68. Влияние положения центра на результаты приведения к этому центру системы сил в пространстве. Инварианты системы сил Положим, что задана система сил Pg.....Р„, произвольно расположенных в пространстве. Выберем в пространстве два различных центра приведения 0 и 0 (рис. 123). Полученные нри приведении к этим центрам силы R* и R* равны главному вектору заданных сил: RI = 2P/; R2 = 2Pb 1- е. r;=:R2 = r*. или R* = const. (58.1) Модуль и направление силы, равной главному вектору заданных сил R* и получаемой при приведении системы сил к некоторому центру, не зависят от положе- 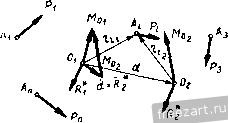 Рис. 12а ния этого центра, т. е. главный вектор данной системы сил инвариантен по отношению к центру приведения. Установим зависимость между главными моментами системы сил относительно центров приведения Oj и Oj. Найдем эти главные моменты (см. § 48): Мо=2<- ХР,. здесь г^ - радиус-вектор точки приложения силы Р, относительно центра приведения Oj , - радиус-вектор точки приложения силы Pj относительно центра приведения О^-Проведем из центра приведения О, в центр радиус-вектор d. Тогда = Ч + г Подставив значение г^. в выражение, определяющее М^, получим Mo.=2-/,XP,-2(r -d)xp, = 2r xp,-2dxP,:= = Sr,. XP,-dx2P,. Мо,=Мо, - dXR*. (58.2) Согласно зависимости (58.2), на рис. 123 главный момент системы сил относительно первого центра Мо, представлен как сумма векторов d X R2 и М^,. При этом вектор d X R2 представляет собой момент силы R*, приложенной в центре 0, относительно центра О,. Этот вектор направлен перпендикулярно плоскости, в которой лежат векторы d и R*, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу R*, направленной по отношению к центру Oj против движения часовой стрелки. Зависимость (58.2) можно сформулировать следующим образом: Главный момент системы сил относительно второго центра приведения равен разности главного момента этих сил относительно первого центра приведения и момента силы, равной главному вектору этой системы сил, приложенной во втором центре приведения, относительно первого центра. Из формулы (58.2) следует, что при перемещении Центра приведения по прямой, имеющей направление главного вектора, главный момент заданной системы сил остается неизменным как по модулю, так и по направлению. Действительно, если центры 0 и Oj лежат на прямой, параллельной главному вектору, то Oj02 = d и R* являются параллельными векторами, а потому dXR* = 0 и Мо=Мо. 8 случае, если главные моменты заданной системы сил относительно произвольно выбранных центров приведения геометрически равны между собой, то рассматриваемая система сил приводится к паре сил. Действительно, при Мо,=Мо2==.. .=1Ло имеем d X R*==0. Так как векторное произведение d X R* равно нулю при любых значениях d, то R* = 0 при }ЛоФО, т. е. силы приводятся к паре сил (§ 54). Умножив скалярно обе части равенства (58.2) на главный вектор R* = Ri==R2, получим: RMo=RMo-R(dxR;). R* (d X Rj) = 0. так как Rj ± (d X R). поэтому R* IAq = R* Mp, т. e. R* Mo = const. (58.3) Полученный результат показывает, что скалярное произведение главного вектора на главный момент данной системы сил инвариантно по отношению к центру приведения. Выразив скалярное произведение (58.3) через проекции перемножаемых векторов на координатные оси, получим XMj, + YMy -Ь ZM == const. Итак, для любой системы сил имеются два основных инварианта, т. е. две величины, не зависящие от положения центра приведения. Первым (векторным) инвариантом системы сил является главный вектор системы сил, а вторым (скалярным) инвариантом является скалярное произведение главного вектора на главный момент этой системы. Выше получена формула (57.8) для вычисления наименьшего главного момента: Так как числитель и знаменатель этой дроби инвариантны по отношению к центру приведения, то наименьший главный момент системы сил М* тоже инвариантен по отношению к центру приведения. Это означает, что проекция главного момента рассматриваемой системы сил относительно любого центра на направление главного вектора есть величина постоянная, не зависящая от положения этого центра (рис. 121). При приведении системы сил к одной из точек центральной оси получаются две инвариантные величины R* и М*. совокупность которых представляет собой динаму. § 59. Уравнения центральной оси системы сил н линии действия равнодействующей Через произвольный центр О, после приведения к которому получены сила R* и пара сил с моментом М = Mq, проведем оси координат X, у, Z (рис. 124). 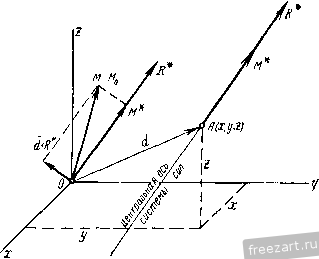 Рис. 124. Возьмем какую-либо точку А{х, у, z) на центральной оси системы сил. Как известно, главный момент относительно этой точки Мд = М* направлен по линии действия силы R*, равной главному вектору заданных сил. Положение центральной ocv (прямой линии) в пространстве определяется двумя уравнениями с тремя переменными координатами х, у, z. Для получения этих уравнений воспользуемся результатами, полученными в § 58. Примем за первый центр начало координат О, а за второй центр-точку А, принадлежащую центральной оси; тогда по формуле (58.2): М* = Мо -dXR*. Спроектируем векторы обеих частей этого равенства на координатные оси x, у, z. Так как произведение d X R* представляет собой момент силы R*, приложенной в точке Л, относительно точки О, то проекции его на оси координат представляют собой моменты этой же силы относительно координатных осей, которые можно выразить аналитически, согласно § 47. Спроектировав, получим: m* = M - {yZ~-zY), m; = m-{zx~xZ), Ml = M - ixY - yX). Так как М* и R* направлены по одной прямой, то одноименные их проекции пропорциональны: или Mx - (yZ - zY) My~(zX - xZ) M:,- (xY-yX) М* X = Y == z ~R- Здесь постоянными величинами являются: главный вектор R* заданной системы сил и его проекции на оси X, Y, Z, проекции My, Ai главного момента М относительно начала координат, а также наименьший главный момент М*. Переменными величинами являются текущие координаты точек центральной оси х, у, г. Два уравнения центральной оси можно получить, приравняв друг другу любые два отношения из четырех. Уравнения имеют более простой вид, если приравнивается одно из первых трех отношений последнему, не содержащему переменных координат. Координаты точек пересечения центральной оси с координатными плоскостями получаются путем приравнивания нулю соответствующих координат. Так, в точке Л^ пересечения центральной оси с плоскостью yOz имеем Xi = 0. в точке А^ 22 = О, а в точке Л3 Уз = 0 (рис. 125). 9*= 131 Если силы приводятся к равнодействующей, то Л1* = 0исила R* является равнодействующей силой R. В этом случае центральная 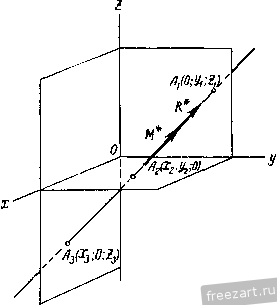 Рис. 125. ось системы сил становится линией действия равнодействующей силы, уравнения которой будут: M - (yZ - zY) My - {zX - yZ) M - {xY-yX) или
(59.2) Здесь X, К, Z - проекции равнодействующей силы на координатные оси; My, М^ - главные моменты заданной системы сил относительно координатных осей. Из трех уравнений (59.2) независимыми будут только два. § 60. Сложение параллельных сил в пространстве. Условия и уравнения равновесия параллельных сил Для сложения параллельных сил Рр Pj.....Р„, приложенных в точках Лд, А2, .... Л„ выберем произвольный центр приведения О. После приведения системы сил к этому центру получим силу, при^юженную в центре приведения и равную главному вектору заданных сил R*, и пару сил с моментом М, равным главному моменту всех сил относительно центра приведения О. Проведем через центр приведения О три взаимно перпендикулярные оси X, у, Z, направив ось z параллельно рассматриваемым силам (рис. 126). Вычислим проекциии главного вектора сил на оси координат: X=Xi = 0; y = Yi = 0; Z = Zi=±Pi, где Z, = -t-P;, если направление силы совпадает с направлением оси z; Z = - Pf, если направления силы Р^ и оси z противопо- 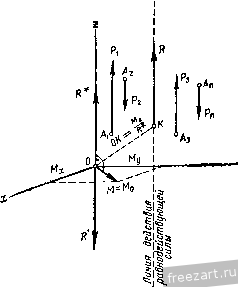 Рис. 126, ложны. Так как = 0 и К = О, то главный вектор R* направлен по оси Z, а его модуль равен абсолютному значению его проекции Z: /?*=z = 12±pj- (60.1) при Z = 2j-(>0 направление главного вектора R* совпадает с направлением оси z, а при Z = 2j -Pj<0 направление R* противоположно направлению оси. Вычислим проекции главного момента относительно начала координат на оси х, у, z как главные моменты сил относительно этих осей: Так как заданные силы параллельны оси z, то Л1 = 0 и главный момент рассматриваемой системы сил лежит в плоскости хОу, т. е. направлен перпендикулярно главному вектору R*. Модуль главного момента М^ равен: При приведении системы параллельных сил в пространстве возможны следующие случаи: 1. Главный вектор R* и главный момент М^, равны нулю. В этом случае силы взаимно уравновешиваются. 2. Главный вектор R* равен нулю, а главный момент М^ не равен нулю. В этом случае силы приводятся к паре сил с моментом М, равным главному моменту этих сил относительно центра приведения. 3. Главный вектор R* не равен нулю, а главный момент М^ или равен нулю или не равен нулю. Если Mq - 0, то силы приводятся к равнодействующей силе линия действия которой проходит через центр приведения О. Если МдфО, то, как указывалось выше, MoJ R*. В этом случае силы приводятся к равнодействующей силе R, линия действия которой проходит через точку К (рис. 126). Из рассмотренных случаев следует, что параллельные силы не приводятся к динаме. Для системы параллельных сил в пространстве имеются два условия равновесия сил: Мо = 0; R* = 0. Если взаимно уравновешивающиеся силы параллельны оси z, то получим а также Жо = /л1-+-Му =0, Ж^ = 51Л1,==0 и Л1у = 2Л1гу = 0, R* =22=0. Таким образом, для системы сил, параллельных оси г, имеем три уравнения равновесия: 22. = о- (60.2) Задача на равновесие параллельных сил, не лежащих в гдной плоскости и приложенных к одному твердому телу, статически ©пре- деленна в том случае, если количество неизвестных в ней не превышает трех. Для системы параллельных сил, приложенной к совокупности двух тел, задача статически определенна при числе неизвестных не больше шести и т. д. § 61. Примеры на приведение системы сил к простейшему виду Пример 32. К вершинам прямоугольного параллелепипеда, ребра которого имеют длину а = 20 см, * = 40 см и с = 30 см, приложены указанные на рис. 127 силы Р^==Ън, Р2 = н, Р^ = 2н, 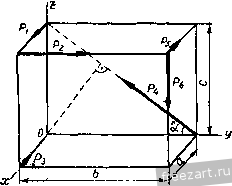 Рис. 127. P=\дн, Р^ = 3н, Pg = 6 (pHc. 127), Требуется привести эту систему сил к простейшему виду. Решение. Предварительно находим: sina = cosa=: . = = 0.6. 50 .= i = o,8. Определяем модуль и направление главного вектора системы сил по ег проекциям на координатные оси: Х = Р,- .р, = 5 -2 -3 = 0, К = Рз cos а = 8 - 10 0.8 = О, Z= P4Sina - Pg == 10 0,6 - 6 = 0, fi* = YX+Y-\-Z = 0. Определяем модуль и направление главного момента системы сил относительно начала координат по его проекциям на координатные оси. равным главным моментам сил относительно этих осей: М^=- - р2с + РфП1Х - Рф = = 8 . 30 + 10 40 0.6 - 6 40 = - 240 сл; 1Л^р^с - Р^с-\-Р^а = Ъ 30 - 3 30 + 6 . 20= 180 см, М, = Р2а--Рф = 20 + 3 . 40 = 280 см; Мо == VmI + + = V (- 240)2 + 1802 + 2802 = 41 о и м; cos(Mo, i) = cos(Mo, j) = - = = 0,439; cos(Mo. к) = -4 = -щ- = 0,683. Полученные результаты показывают, что заданная система сил приводится к паре сил. Модуль момента пары Л1 = Л1о = 410н. см. Направление момента составляет с координатными осями углы, определяемые найденными косинусами. Пример 33. К вершинам прямоугольного параллелепипеда, ребра которого имеют длину а = 20сл, *==30сл, с = 40сл<. приложены указанные на рис. 128 силы Р, = Ан, Р^Юн, и Яз = 5 W. Требуется привести эту систему сил к простейшему виду. Решение. Определяем модуль и направление главного вектора системы сил по его проекциям на координатные оси: Х = Рг = 4н, К = Р2=10н, Z = -Р, = -5и, 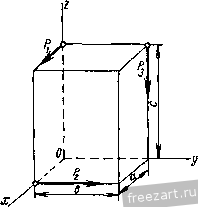 Рис. 128. P* = yA2+K2 + Z2 = {/l41= 11.87 k. cos (Г. i) = -= 0.337, cos (Г, j) = =0,842. cos(R*. к) = - = - 0.421. 1 ... 10 11 12 13 14 15 16 ... 44 |
 |
 |