

 |
 |
|
Навигация
|
Главная » Мануалы в зависимости от модулей и точек приложения этих сил воз- можны следующие случаи: 1. Силы R2 и R3 не равны по модулю. Предположим, что в рассматриваемом случае (рис. 140) > R. Тогда равнодействующая R заданных сил имеет модуль R = R - R и направлена в сторону больщей силы Rg. Точка С, в которой приложена равнодействующая сила R, находится на продолжении отрезка Sgs. за точкой приложения большей силы, причем В,С 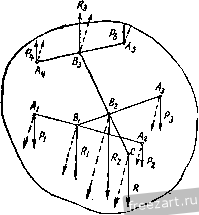 Точка С называется центром параллельных сил. Через эту точку обязательно проходит линия действия равнодействующей заданной системы параллельных сил, если, не изменяя модулей сил, поворачивать линии действия сил вокруг точек их приложения на один и тот же угол в одну и ту же сторону <рис. 140). Действительно, все приведенные равенства, определяющие модули и точки приложения равнодействующих сил R Rg, р(з, R. при повороте сил остаются справедливыми. 2. Силы R2 и R3 равны по модулю, но их линии действия не совпадают. В этом случае заданные силы приводятся к паре сил. 3. Силы R2 и R3 равны по модулю и их линии действия совпадают. В этом случае заданные силы взаимно уравновешиваются. Система параллельных сил, направленных в одну сторону, не может уравновешиваться или приводиться к паре сил. Эта система всегда имеет равнодействующую. ?ис. 140. § 65. Формулы радиуса вектора и координат центра параллельных сил Рассмотрим систему параллельных сил Pj, Pj Р„, приложен- ных в точках А-, А^, .... Л„, приводящуюся к равнодействующей R, приложенной в точке С (рис. 141). Положение центра параллельных сил С определится его радиусом-вектором Гс относительно начала координат О или тремя координатами Xq, У(., Zq. Положение точки приложения каждой силы определяется радиг-сом-вектором г,- или координатами х^, у,-, z, где г=1, 2.....п. На основании теоремы Вариньона о моменте равнодействующе относительно любого центра (§ 56) приравниваем момент равнодействующей относительно центра О геометрической сумме моментов, составляющих сил относительно этого центра: или согласно § 44 Mo(R)=-SM, ГсХР=2Г;УР;. 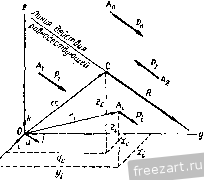 Рис. 141. Введем единичный вектор и, параллельный линиям действия сил. Тогда получим Р, = иР;. где Pi-алгебраическое значение силы. R = 2P = u2Pi. Подставив значения Р, и R в выражения моментов, будем иметь Гс X nlPi = X иЯ,.. Переместим скалярные множители в векторных произведениях: Tci Ха = 2г,.Р,- X U, (CcPi- 2г,Я,)Х u = 0. или Вектор U может иметь любое направление, так как, согласно свойству центра параллельных сил, линии действия сил можно поворачивать. Следовательно, TcPi - LTiPi = 0. Из этого равенства получим формулу, определяющую радиус-вектор центра параллельных сил: Гс = Щ. (65.1) 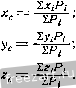 Спроектировав векторы левой.и правой частей равенства (65.1) на оси координат, получим формулы для вычисления координат центра параллельных сил: (65.2) В формулах (65.2) числителем и знаменателем каждой дроби является алгебраическая сумма. Координаты точки приложения каждой силы имеют тот или другой знак, и параллельные силы, направленные в одну сторону, считаются положительными, а направленные противоположно - отрицательными. Таким образом, координаты JCj, У;, и значения сил Р; в этих формулах являются алгебраическими величинами. Выбор направления, вдоль которого параллельные силы считаются положительными, произведен и на результатах вычисления координат по формулам (65.2) не отражается. § 66. Центр тяжести твердого тела Силы притяжения отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы т сравнению с радиусом Земли, то эти силы можно считать параллельными. Равнэдействующая этих параллельных сил, равная их сумме, есть вес тела, а центр этой системы параллельных сил, в котором приложен вес тела, называется центром тяжести тела. В твердом теле центр тяжести занимает вполне определенное положение, которое не зависит от расположения рассматриваемого тела в пространстве. Обозначим силы притяжения отдельных элементарных частиц тела к Земле AGj, AOj..... G, вес тела G, координаты его центра тяжести х^. Ус c координаты любой частицы твердого тела--х-, у,-, z (рис. 142). Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил. Для центра тяжести формулы (65.1) примут вид: Zr = а (66.1) где суммирования распространены на все частицы твердого тела. В этих формулах алгебраическими величинами являются только координаты точек, а значения ДО; всегда положительны, так как все силы направлены в одну сторону. По формулам (66.1) можно также вычислять координаты центра тяжести тела, разбивая его не на элементарные частицы, а на от-г 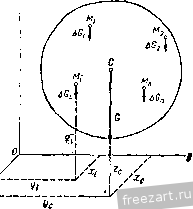 Рис. 142. дельные части веса 0(, координаты Х;, у;, 2 центров тяжести которых известны. Определим положение центра тяжести однородного тела. Вес однородного тела определяется формулой G = {V, где V - объем тела, 7 - вес единицы объема. Аналогично вес каждой частицы определяется по формуле ДО,- = 7Д'У/> где Дг ; - объем элементарной частицы тела. Обозначим X;, 2; координаты центра тяжести этой частицы. Подставив эти значения, получим xihGi xcilvi tXihvi или аналогично получим Ус - -17-> --V- (66.2) Центр тяжести однородного тела, заполняющего некоторый объем, называется центром тяжести этого объема. § 67. Центр тяжести плоской фигуры. Статический момент площади плоской фигуры относительно оси Однородное тело, имеющее форму тонкой пластинки, можно рассматривать как материальную плоскую фигуру. Положение центра тяжести плоской фигуры определяется двумя координатами и у^, (рис. 143). Вес однородной пластинки выразим формулой О = шр, где F - площадь плоской фигуры, ш - вес единицы ее площади. Разобьем площадь фигуры на элементарные площадки. Вес каждой площадки определится по формуле ДО-шД ;, где Д^ - ее площадь. Обозначим х;, у^ координаты центра тяжести элементарной площадки Ml. Тогда координаты центра тяжести фигуры определятся при помощи формулы (66.1) х^ДО,- x,o>AFi -XiAFi У ~ G ~~ шГ Таким образом. (67.1) 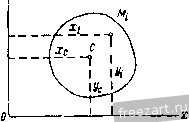 Рис. 143. где суммирования распространены на все элементы площади. Эти формулы показывают, что координаты х^ и у^ центра тяжести однородной пластинки не зависят от постоянной ш, характеризующей вещество пластинки. Центр тяжести однородной пластинки называют центром тяжести площади этой пластинки. Сумма произведений элементарных площадей, входящих в состав площади фигуры, на алгебраические значения их расстояний до некоторой оси, называется статическим моментом площади плоской фигуры относительно этой оси. Обозначая 5 и статические моменты площади плоской фигуры относительно осей х и у, на основании (67.1) имеем S==ZyiPi = Pyc Sy = xAFi = Fxc. (67.2) Таким образом, статический момент площади плоской фигуры относительно оси равен произведению площади фигуры на алгебраическое значение расстояния от центра тяжести до этой оси. Статический момент площади плоской фигуры относительно оси измеряется в см. И А. А. Яблонский Если известны статические моменты площади плоской фигуры относительно координатных осей, то координаты ее центра тяжести можно определить по формулам: (67.3) Очевидно, что статический момент площади плоской фигуры относительно оси, проходящей через центр тяжести фигуры, равен нулю. § 68. Центр тяжести линии Определим положение центров тяжести однородных тел, имею- щих большую протяженность при поперечного сечения. Рассмотрим, 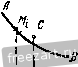 2i \?с сравнительно малой площади напри.мер, кусок однородной тонкой проволоки постоянного сечения, ось которой расположена по дуге кривой АВ (рис. 144). Вес проволоки выразим формулой G = pL, где L - длина линии АВ, р - вес единицы длины проволоки. Разобьем линию АВ на элементарные участки Ml длиной Д/j. Вес каждого участка определится по формуле: значим Xi, \)i. Рис. 144. Координаты центра тяжести элементарного участка обо-2,-. Тогда координаты центра тяжести С рассматри- ваемого куска проволоки определятся по формулам (66.1): хс = - пли (68.1) где суммирования распространены на все элементы проволоки. Формулы (68.1) показывают, что координаты центра тяжести не зависят от постоянной р, характеризующей вещество проволоки. Центр тяжести однородной тонкой просолоки постоянного сечения, ось которой совпадает с некоторой линией, называется центром тяжести этой линии. § 69. Вспомогательные теоремы для определения положения центра тяжести При вычислении координат центров тяжести пользуются различными приемами, позволяющими упростить вычисления. Рассмотрим четыре вспомогательные теоремы, упрощающие в некоторых случаях нахождение центров тяжести. Теорема 1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Рассмотрим однородное тело, имеющее ось симметрии (рис. 145). Совместим с осью симметрии одну из осей координат, например ось Z, и определим две координаты центра тяжести однородного тела по формулам (66.2): 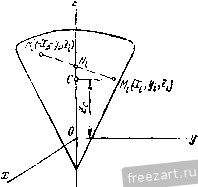 Рис. 145. Возьмем в этом теле любые две точки М. и М\, расположенные симметрично относительно оси Z. Выделим около них равные элементарные объемы Д-у^. Точки и М\ лежат на одном перпендикуляре к оси Z, на равных расстояниях от этой оси, т. е. MJ<11 = M\Ni (рис. 145). Следовательно, координаты и у,- этих точек равны по величине и противоположны по знаку. Разбив все тело на пары симметрично расположенных и равных элементарных объемов, составляем произведения х^Дг ,- и суммируем их. Сумма слагаемых, относящихся к одной паре, равна нулю, так как объемы Дг ,- равны, а координаты х, равны по величине, но имеют противоположные знаки. Из этого следует, что равна нулю и сумма, содержащая все элементарные объемы тела, т. е. 2.ij = 0 и аналогично 2УгДг;; = 0. Подставив эти значения в формулы (66.2), получим: с - у - Ус --у-= о. Так как = О и - 0. то центр тяжести тела лежит на оси z, являющейся осью симметрии тела, и его положение на этой оси определяется лишь одной координатой: Применяя эту теорему к плоской фигуре или линии, легко установить, что если плоская фигура или линия имеет ось симметрии, то ее центр тяжести лежит на этой оси. Теорема 2. Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости. 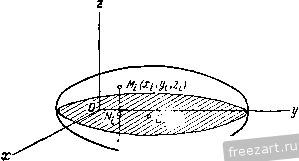 Рис. 146. На рис. 146 изображено тело, имеющее плоскость симметрии; сечение тела этой плоскостью заштриховано. Расположим оси х а у в плоскости симметрии, а ось z перпендикулярно к ней. Возьмем в этом теле две точки Мц и М', симметрично расположенные относительно плоскости хОу. Выделим около них равные элементарные объемы Дг ;. Точки и М\ лежат на одном перпендикуляре к плоскости хОу, на равных расстояниях от этой плоскости, т. е. i - MNi (рис. 146). Следовательно, координаты 2 этих точек равны по величине и противоположны по знаку. Суммируя произведения ггДг ;, получим z,.v - O, где суммирование распространено на все элементарные объемы. Вычислим координату z. центра тяжести рассматриваемого однородного тела по формуле (66.2): Zf. - - Полученный результат показывает, что центр тяжести рассматриваемого тела находится в плоскости симметрии. На основе рассмотренных теорем можно определить положения центров тяжести некоторых симметричных линий, фигур и тел: 1) центр тяжести отрезка прямой лежит в его середине; 2) центры тяжести окружности, площади круга, поверхности и объема шара находятся в их геометрических центрах; 3) центры тяжести периметра и площади параллелограмма, ромба, прямоугольника и квадрата лежат в точках пересечения их диагоналей; 4) центр тяжести периметра и площади правильного многоугольника находится в центре вписанного (или описанного) круга. Теорема 3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести*. Пусть плоская фигура площадью F вращается вокруг оси у, лежащей в плоскости фигуры и не пересекающей ее. При вращении вокруг оси у контур этой фигуры описывает некоторую замкнутую поверхность, называемую поверхностью вращения. Тело, ограниченное этой поверхностью, называется телом вращения (рис. 147).
Рис. 147. Объем этого тела вращения определим, как сумму бесконечно большого числа объемов элементарных круговых колец, образованных вращением вокруг оси у бесконечно малых площадок ДР. Радиус каждого кольца равен расстоянию этой площадки от оси у, т. е. координате ДГ;. Объем элементарного кольца Объем тела вращения Здесь суммирование распространено на все площадки, входящие в состав данной плащади F. * Эта и последующая теоремы выведены математиком IV столетия Паппом, а в XVII столетии они вновь были применены в работах Гюльдена о центре тяжести. Сумму XiAFf можно определить из формулы (67.1): Хс = р-. 2j Xi = Xf.F. Подставив это значение в выражение, определяющее объем тела вращения, получим: V=2KXcF, (69.1) где 2kXq - длина окружности, описанной центром тяжести фигуры. Теорема 4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но ее не пересекающей, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести. Пусть кривая АВ длиной L А вращается вокруг оси у, лежащей в плоскости этой кривой, но не Хс \ пересекающей ее. При вращении С \ вокруг оси у эта кривая опишет \ некоторую поверхность вращения в (рис. 148). Разобьем 1ривую на бесчислеи- ное множество бесконечно малых элементов длиной Д/. Поверхность, описанную каждым элементом, мож-но принять за поверхность усеченного конуса. Как известно из геометрии, площадь боковой поверхности усеченного конуса равна произведению-длины окружности среднего сечения на длину образующей. Поэтому площадь поверхности, образованной вращением элемента кривой Д/; можно определить по формуле Д^; = 2nxi М^, где Xi - радиус окружности, равный расстоянию середины элемента от оси у. Площадь поверхности вращения здесь суммирование распространено на все элементы Д/ кривой АВ. Сумму XiMi определим из формулы (68.1): у. X, Mi = i : XiM = xL. Подставив это значение в выражение, определяющее площадь поверхности вращения, получим F = 2tzXcL. (69.2) 1 ... 13 14 15 16 17 18 19 ... 44 |
 |
 |