

 |
 |
|
Навигация
|
Главная » Мануалы Обозначив i, j и к - единичные векторы, направленные по осям х, у \1 Z, а. X, Y и Z - проекции силы на эти оси, получим Р=Р,+ Ру + Р.> PiA-; P = JK; P, = kZ; поэтому PIA + jK + kZ. (37.1) Равенство (37.1) представляет собой формулу разложения силы на составляющие по осям координат. /Г Рис 99. Проекция силы на каждую координатную ось определяется произведением модуля силы на косинус угла между направлениями оси и силы: А- = Р cos (Р, i); Y = P cos (Р, j); Z = Р cos (P, к), где (P, i), (P, j) и (P, k) - углы, заключенные между направлением силы Р и направлениями осей х, у ш г. Если известны проекции силы на три взаимно перпендикулярные оси X, у У1 Z, то модуль и направление силы определяются по следующим формулам: (37,2) P = y2K24-Z2, cos(P, 0 = ; cos(P, i) = l-; cos(P, k) = . (37,3) § 38. Аналитический способ определения равнодействующей системы сходящихся сил в пространстве. Уравнения равновесия сил Равнодействующая сходящихся сил Pj, Pj, . равна геометрической сумме этих сил: R=PiP2-b ... Ч-Р„. Р„ (рис. 100) Проекция равнодействующей на каждую из координатных осей равна алгебраической сумме проекций всех составляющих: Х = Х, + Х2 ... + . i +-2 + +Уп- \ (38-1) Z = Zi +Z, + ... +z . где проекции сил вычисляются по формулам: Л-, = Pi cos (Pi, i) Ki = PiCos(Pi, j) Zi = PiCos(Pi. k) X = Pj cos (P2. J); ...; K2 = P2Cos(P2, j); Z2==P2Cos(P2. k); Формулам (38.1) можно придать вид: причем 1, 2, .... я. Вычислив проекции равнодействующей X, V и Z, найдем модуль и направление равнодействующей по формулам (37.2) и (37.3): P==/2-f-K2Z2. X = P cos(P , i); K = P cos(P , j); Z = P cos (P , k). (38.2) cos (R. i) = ; cos (R, j) = -J-; cos (R, k) = В случае, если силы взаимно уравновещиваются, их равнодействующая R равна нулю. Так как Р=: /Л'з + К^ -f Z, то X = Q; Y = 0 и Z = Q. 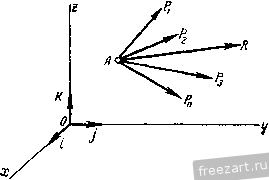 Рис. т. Таким образом, для сходящихся сил в пространстве имеем следующих три уравнения равновесия: Xi-j-X2+ ... ~\-Х„ = 0 или Х^=0. Kj К2 -+-...+ К„ = О или 2 = 0. Zi -+-Z2 + ... -+-Z =0 или 2z, =0. (38.5) При помощи уравнений (38.3) можно решать вадачи на равновесие сходящихся сил, если число неизвестных величин в задаче не превышает трех. § 39. Примеры на равновесие сходящихся сил Пример 29. Груз А весом G = 20 крепленной в точке В, и удерживается плоскости BCDE силой Q, направленной по линии наибольшего ската этой плоскости. Определить наименьшее значение этой силы, если коэффициент сцепления между телом и плоскостью /сц=0,2, угол наклона плоскости к горизонту а=45° и угол, составленный веревкой АВ и горизонтальной прямой ВС, Р = 30° (рис. 101а). Решение. Рассматриваем равновесие сил. приложенных к грузу А: заданных сил - веса О. силы Q. а также реакций связей - реакции веревки S. нормальной реакции плоскости н привязан к веревке, за-на шероховатой наклонной 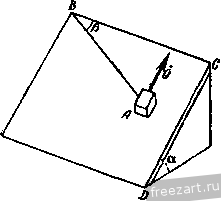 Рис. 101а. N и максимальной силы сцепления Р™ц'. направленной противоположно направлению возможного скольжения груза. Возможное 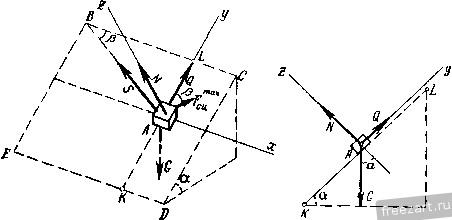 Рис. 1016. Рис. 101в. движение груза при недостаточной величине силы Q должно происходить по дуге окружности с центром в точке В, а сила сцепления должна быть направлена по касательной к этой окружности, т. е. перпендикулярно к радиусу ВА (рис. 1016). В момент предельного состояния покоя FTa = fcu- Три неизвестные величины Q, N и S можно определить из трех уравнений равновесия сходящихся сил (38.5). Проводим оси координат, как показано на рис. 1016, в и составляем уравнения равновесия сил: 2£ = 0; F .ScosB = 0; =0; Ffucosp + Q + Ssinp -Gsina = 0; 2 2; =0;. Л/ -О cos а = 0. Из уравнения (3) определяем ЛА: ЛГ= О cos а = 20=10/2= 14,14 н. (1) (2) (3) Из уравнения (1) находим S: -/c A/tgp = 0,2. 10/2.- = - cos р Из уравнения (2) определяем Q: Q = ~ ДцЛ/ cos р - S sin р + О sin а = = -0,2. 10/21- 20 1,63 . = 10,87 н. Пример 30, Горизонтальный провод АЕ, натяжение которого равно 300 н, подвещен к вертикальному столбу АВ, укрепленному оттяжками АС и AD, расположенными симметрично относительно плоскости ВАЕ. Известно: АВ=6 м, ВС=В04,Ъм, / CBD:=m  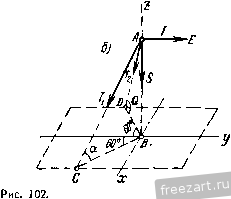 Определить натяжение оттяжек и усилие в столбе (рис. 102, а). Рещение. Рассмотрим равновесие сил, приложенных к узлу А: заданной силы - реакции Т провода АЕ, реакции S столба АВ и реакций и 1 оттяжек АС и AD. Три неизвестные силы S, Tj и Tj определим из трех уравнений равновесия этой системы сходящихся сил: Для этого проведем оси координат из точки В, направив ось z вдоль В А, ось у - параллельно ЛЕ и ось х - перпендикулярно к осям у п Z (рис. 102, б). Приложим к узлу А все действующие на него силы, направив их от узла, т. е. предположив, что все элементы растянуты. При проектировании сил Tj и Tg на оси хну применим двойное проектирование, так как углы, составленные этими силами с осями л: и у, не даны. Спроектируем сначала каждую из этих сил на плоскость хВу и полученную проекцию спроектируем на соответствующую ось. Вычислим предварительно: СВ 4,5 с cos а =-= , = 0,6. СА 1/62+4,52 ВА 6 по sma=i=--- =n,R. СА /6=+ 4,5= Составим уравнения равновесия: А', = 0; cos а cos 30° - cos а cos 30° == 0; (1) 2 К, =0; - Ti cos а cos 60° - Гз cos а cos 60° + Г = 0; (2) 2 Z = 0; - cos (90° - a) - cos (90° - a) -S = 0. (3) Из уравнения (1) получим Из уравнения (2) найдем эти силы: - гГ, cos а cos 60° -h Г = 0. Т - -rjnn и 1 ~ 2 cos а cos 60 ~ 2 0,6 0,5 ~ T2 = 7i = 500 н (натяжение симметричных оттяжек одинаково). Из уравнения (3) определим S: - 2riSina--5 = 0. 5= -2r,sina = -2 500 0,8 = -800 . Вертикальный столб АВ сжат. Пример 31. Определить усилия в стержнях фермы, изображенной на рис. 103а, если на узел В фермы действует вертикальная сила Pj = 40 кн, на узел С - горизонтальная сила 20 кн, направленная вдоль стержня CD. Размеры указаны на рисунке. Решение. Для определения усилий в стержнях фермы восполь-вуемся способом вырезания узлов. Так как силы, действующие на каждый из узлов фермы, взаимно уравновешиваются то, вырезая отдельные узлы фермы, составляем по три уравнения равновесия сил, действующих на каждый узел. Узлы фермы вырезаем в такой последовательности, чтобы число неизвестных сил в рассматриваемом узле не превышало трех. Так же, как и при определении усилий в стержнях плоских ферм, все стержни фермы условимся считать растянутыми; знак минус у вычисленной реакции стержня означает то, что стержень сжат. Для определения усилий в стержнях рассматриваемой фермы будем вырезать последовательно узлы А, В. С п D (рис. 1036). В точках Е, F, К, L показаны составляющие реакции опор R Rf, Ri, R Rfj R/f,. Ra-j. уравновешивающие реакции стержней. Как показано ниже, усилия во многих стержнях рассматриваемой фермы равны нулю. Поэтому не будем определять предварительно всех косинусов углов, составленных силами с осями координат, и проекции некоторых сил запишем в уравнения равновесия в общем виде, не определяя по чертежу знака проекций. 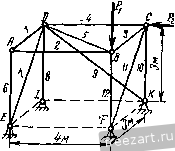 Рис. 103а. 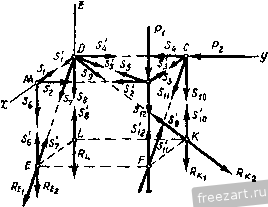 Рис. 1036. Очевидно, что и составляющие реакций опор, направленные вдоль стержней с нулевыми усилиями, будут равны нулю. 2к, =0 2z.=o Узел А - S, = Q; 5i = 0; s2 = 0; Так как узел А не загружен внешней силой, а силы Sj, не лежащие в одной плоскости, не могут уравновешиваться, равны нулю. Узел В 2Х,=:0; - 5з4-5cos(s5, i) = 0; =0; -52 4-55COs(s5, j) = 0; 2Zi=:0; -Pi -5i2=:0; 5i2 = -Pi = -40 km Из уравнения (2) находим 55 cos (S5, j) = 52 = 0; 55 = 0. Из уравнения (1) находим 5з = 55Соз(85. j) = 0. 5з = 0. Узел С Xi = 0; 5; + 5iiCos(Sn, i) = 0; =0; -54 -Р2 = 0; 5= -Р2 = -20 км; 2 = 0; - 5io Ч- 5,1 cos (Sip к) = 0. Из уравнения (1) находим: SiiCos(Sn. = -5з = 0; Sii = 0. Из уравнения (3) находим: 5io-5i,cos(Sii, к) = 0; 5,о = 0. Узел D Xi=:0; 5;+ 55cos(Ss. i) + 57Cos(s7, i) = 0; 2 Кг = 0; 54 + 55 cos (Sy J) + 59 cos (s9. j) = 0; 2 Zj = 0; - 58 + 5; cos (S, k) + 5 cos (s9, k) = 0. Из уравнения (1) находим: 57Cos(s7, i) = -5l -S5Cos(s5, i) = 0; 57 = 0. Из уравнения (2) находим: S2 и Sg то они (2) (3) (1) (2) (3) (2) (3) Так как <? -S-S,cos{S j) 9 - cos (Sg, j) 55=0 и 54 = -20 km, COS(Sa, j) = -7== = 0,8. / 5a = cos (s9, j) :=25 km. Из уравнения (3) находим 5g = 57008(87, k)--5gCOs(So, к). Так как 7 = 0, cos(S9, к) = - - = - 0,6; 58 = 9005(89, к) = -25-0,6 = -15 кн. Таблица усилий Таблица 2
Основываясь на результатах расчета, можно установить следующее: 1. Если в незагруженном узле фермы сходятся три стержня, не лежащих в одной плоскости, то усилия в каждом из этих стержней равны нулю (узел А, стержни /, 2 и 6). 2. Если в некотором узле фермы все внешние силы и все стержни, кроме одного, лежат в одной плоскости, то усилие в стержне, не лежащем в этой плоскости, равно нулю (узел С, стержень 11 при S3 = о). Эти соображения, дающие возможность определить без вычислений стержни с нулевыми усилиями, значительно упрощают определение усилий в стержнях пространственных ферм. ГЛАВА VII ТЕОРИЯ ПАР СИЛ В ПРОСТРАНСТВЕ § 40, Момент пары сил Числовое значение момента пары сил на плоскости равно произведению одной из сил пары на ее плечо, а знак момента определяется направлением, в котором пара сил стремится вращать плоскость. В пространстве направление вращения, вызываемого парой сил в плоскости ее действия, не характеризуется знаком ее момента, так как смотря на плоскость действия пары сил с различных ее сторон, можно видеть одну и ту же пару стремящейся вращать плоскость в различных направлениях. Момент пары сил в пространстве рассматривают как вектор (рис. 104а и б), направленный по перпендикуляру к плоскости заданной пары сил в такую сторону, чтобы, смотря навстречу этому вектору, видеть пару стремящейся вращать плоскость против движения часовой стрелки. Этот вектор может быть приложен в любой точке плоскости действия пары, так как пару в этой плоскости можно переносить. 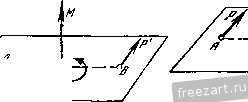 Рис. 104а. Рис. 1046. Модуль вектора момента равен произведению одной из сил пары на ее плечо: M = Pd. Таким образом, вектор момента определяет не только числовое значение момента, а также плоскость действия пары сил и направление, в котором пара стремится вращать эту плоскость. § 41. Теорема о возможности переноса пары сил в любую плоскость, параллельную плоскости действия пары Заданную пару сил, не изменяя ее действия на твердое тело, можно перенести в любую плоскость, параллельную плоскости действия этой пары. Положим, что к некоторому твердому телу приложена пара сил Р, Р' с плечом АВ, расположенная в плоскости /. Проведем плоскость , параллельную носкости /, и возьмем в этой плоскости отрезок DC, равный и параллельный отрезку АВ, и приложим к концам этого отрезка по две взаимно уравновешивающиеся силы, равные по модулю и параллельные силам рассматриваемой пары (рис. 105а): Pj = Pj 3 = 4 = р- Сложим силу Р, приложенную в точке А, с силой Pg, приложенной в точке С. Их равнодействующая R = P-\-P, приложена в точке К, делящей отрезок АС пополам, т. е. в точке пересечения 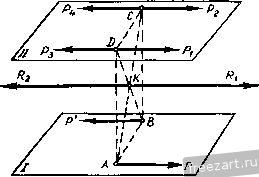 диагоналей параллелограмма ABCD. Сложив силу Р', приложенную в точке В, с силой Р3, приложенной в точке D, получим их равнодействующую R2 = P~\-Pv которая также приложена в точке К. Силы Ri и Rg, как равные по модулю и направленные по одной прямой в противоположные стороны, взаимно уравновешиваются. Остаются силы Pj и Р4. составляющие пару сил с плечом DC расположенную в плоскости , параллельной плоскости /. Эта пара сил, эквивалентная заданной паре сил, стремится вращать плоскость в том же направлении, в котором стремится вращать плоскость / заданная пара сил, а момент эквивалентной пары сил численно равен моменту заданной пары сил: Таким образом пару сил можно переносить из одной плоскости в другую, параллельную ей плоскость. § 42. Теорема об эквивалентных парах Пари сил эквивалентны, если их моменты геометрически равны. Положим, что даны две пары сил, лежащие в различных плоскостях и имеющие геометрические равные моменты Mi = M2. Докажем, что эти пары эквивалентны.   Рис. 1056. Так как моменты М, и М2 пар Р, Р' и Q, Q геометрически равны, т. е. не только равны по модулю, но и совпадают по направлению, то плоскость / действия пары Р, Р' и плоскость действия пары Q, Q параллельны, и направления, в которых пары сил стремятся вращать эти плоскости, совпадают (рис. 1056). Согласно предыдущей теореме, пару сил Р, Р' с плечом АВ в плоскости / 1 ... 7 8 9 10 11 12 13 ... 44 |
|||||||||||||||||||||||||||||||||||||||||||
 |
 |