

 |
 |
|
Навигация
|
Главная » Мануалы как проекции сил Sg и Sg на эту ось равны нулю: 2К,=:0; /?д + 57соз45= = 0; S, = - cos 45 = - 28,3 к№. Для определения усилия составим уравнение моментов этих же сил относительно точки Риттера L, в которой пересекаются линии действия сил Sg и Sj: 58 = -Pfi-f- -40 tcH. Знаки полученных ответов показывают, что стержень 6 растянут, а стержни 7 и 8 сжаты. Изложенный способ определения усилий в стержнях фермы предложен Риттером и носит название способа Риттера. Для определения усилий в стержнях рассмотренной фермы по способу Риттера использована II система уравнений равновесия плоской системы сил.
Рис. 73а. Пример 17. Определить усилия в стержнях 8, 9 м ]0 фермы, изображенной на рис. 73а, если Р, = 40 кн, = 80 км, Q = Q = 10 км, Q2 = 20 кн, АВ = Аа; KD = 2a. Решение. Прежде всего определим реакции опор фермы Хд, Уд. Rb (рис. 736). Для этого составим три уравнения равновесия Сил, действующих на ферму: 2 = 0; - Р,2а - Р^За + /?д4а - Qa /2 - Q2a /2 = 0; 2 а:, = 0; - cos 45 - cos 45° - Qjcos 45 = 0; = (Q, + Q2 + Q3) cos 45 = 40 = 28,3 кн. 2 К; = 0; Кд-Pj-Рз + Rs-Qi cos 45°-cos 45°-Q3 cos 45° = 0: Кд = Pi + + (Qi + Q2 + Оз)cos 45° - /?д = 54,2 к . Для определения усилий в стержнях 8, 9 а 10 проведем сечение /-/. Мысленно отбросим левую часть фермы, заменив ее действие на оставшуюся часть реакциями разрезанных стержней Sg, S9 и S,o, направив эти силы в сторону отброшенной части (рис. 73в).
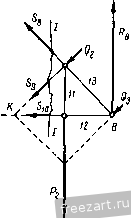 Рис. 736. Рис. 73в. Чтобы определить каждое усилие независимо от двух других, применим III систему уравнений равновесия (§ 21). Составим уравнения моментов сил, действующих на правую часть фермы, относительно точек Риттера /С, В и L, в которых пересекаются по две линии действия усилий: 2 М; = 0; Sa У 2 - Рф + Рд2а - Qa /2 = 0; .<и-7г=-hQ4 = - 66,5 к . /2 Y2 2Мгд = 0; 59a]/ 2 + Q2al/2 + p2u = 0; 5<, = -((32 + у|) = -76.6 кн. 5io = /?B -32 = 80 кн. § 27. Условие равновесия сил, приложенных к рычагу. Устойчивость при опрокидывании. Коэффициент устойчивости Рыяагом называется твердое тело, имеющее неподвижную ось вращения и находящееся под действием сил, лежащих в плоскости, перпендикулярной к этой оси. Положим, что к рычагу в точках А^, Лз.....Л„ приложены задаваемые силы Pj, Pj, . .., Р„, лежащие в плоскости чертежа, а ось рычага пересекает эту плоскость в точке О, которую назовем опорной точкой (рис. 74). 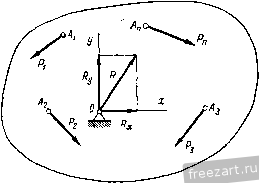 Рис. 74 Реакция R оси рычага, уравновешивая задаваемые силы, лежит в их плоскости, но направление ее не известно. Разложим реакцию оси на две составляющие и Ry и выведем уравнения равновесия сил, действующих на рычаг. На основании уравнений равновесия плоской системы сил имеем: п 1 = 1 (27.1) (27.2) (27.3) Здесь Xi и 2 - суммы проекций задаваемых сил, прило- i = l 1 = 1 женных к рычагу, на оси х а у; к Ry - проекции реакции оси п рычага на эти оси; М, - сумма моментов задаваемых сил отно-i = i сительно опорной точки. Третье уравнение, не содержащее реакции оси рычага, и выражает условие, которому удовлетворяют задаваемые силы, уравновешиваемые реакцией оси рычага. Это условие формулируется так: при равновесии сил, приложенных к рыяагу, алгебраическая сумма моментов всех задаваемых сил, действующих на рычаг, относительно опорной точки равна нулю Из уравнений (27.1) и (27.2) определяется реакция оси рычага. Из условия равновесия сил действующих на рычаг, -получим условие устойчивости тел при опрокидывании. Положим, что к прямоугольному парал-Рис. 75 лелепипеду (рис. 75) весом О на вы- соте d приложена горизонтальная сила Р, которая может не только сдвинуть тело, но и опрокинуть его вращением вокруг ребра А. Считая, что сила Р недостаточно велика, чтобы сдвинуть тело, рассмотрим ее опрокидывающее действие (см. § 29). Обозначим а расстояние от точки А, изображающей на чертеже ось вращения рычага, до линии действия силы G, которая препятствует опрокидыванию. Составим сумму моментов задаваемых сил Р и G относительно опорной точки А: Mi - Q; Оа- Pd~0, откуда Ga=Pd. Назовем абсолютные величины моментов сил G и Р относительно точки А удерживающим и опрокидывающим моментами: 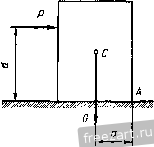 Ga = M Pd = M 1уд, i ч, опр- Тогда на границе устойчивости получим: При устойчивом состоянии тела: Устойчивость при опрокидывании в технике принято определять отношением величины удерживающего момента к величине опрокидывающего момента: опр Это отношение называют коэффициентом устойчивости. Очевидно, что в случае предельной устойчивости коэффициент устойчивости равен единице, а в случае устойчивого состояния А > 1. Определить, опрокинется ли тело под действием силы Р или будет находиться в устойчивом состоянии, можно и графическим путем. Для этого продолжим линии действия сил G и Р до их пересечения в точке К, перенесем силы в эту точку и найдем их равнодействующую R (рис. 76). Продолжая линию действия равнодействующей силы, найдем точку ее пересечения с опорной плоскостью. В рассмотренном примере возможны три случая: 1. Если эта точка лежит слева от ребра А, то состояние тела устойчиво. 2. Если линия действия равнодействующей пересекает ребро А, то состояние тела предельно устойчиво. 3. Если эта точка лежит справа от ребра А, то тело опрокинется. § 28. Примеры на применение условия равновесия сил, приложенных к рычагу Пример 18. Определить вес противовеса Oj, обеспечивающий коэффициент устойчивости нагруженного крана при опрокидывании.
Рис. 76. 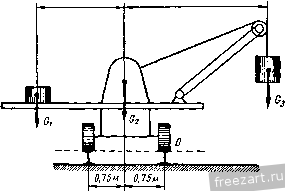 Рис. 77. равный 1,5, если вес крана = 50 кн, вес груза 63 = 40 кн. Размеры указаны на рис. 77. Решение, Предполагаемое опрокидывание крана под действием веса груза G3 является вращением вокруг оси О, совпадающей с пра- вым рельсом. Силами, препятствующими опрокидыванию, являются вес крана Gg и вес противовеса Gj. Определим опрокидывающий момент как абсолютную величину момента силы G3 относительно точки О: Жо р = Оз 1,25 = 40 1,25 = 50 кн-м. Определим удерживающий момент как сумму абсолютных величин моментов сил G, и Gg относительно точки О: = G, 24- Оз - 0,75 = Oi 2 + 50 0,75 = (20, + 37,5) кн м. Воспользуемся коэффициентом устойчивости тела при опрокидывании М опр ЖуД = ftMonp 2GiH-37,5= 1,5 50; Gi= 18,75 кн. Пример 19. Определить минимальную ширину а бетонной плотины прямоугольного сечения по условию устойчивосги при опрокидывании, если высота п.тотины о /г = 3,5 м, вес 1 м^ бетона 7 = 22,5 кн/м^, горизонтальное давление воды на 1 м длины плотины со стороны верхнего бьефа Pi = 45 кн, со стороны нижнего бьефа Р2= 11,25 кн. Расстояния от точек приложения сил Pj и Рз до основания: ft, - \ м. fir, = 0,5 м (рис. 78). Решение. Рассмотрим бетонный массив в форме прямоугольного параллелепипеда, измерения которого равны ft, а и 1 л в направлении длины плотины. Вследствие того, что Pj > Рз и Aj > 3, возможным опрокидыванием плотины будет ее вращение вокруг ребра О. Силой, вызывающей опрокидывание, является сила Pj, направленная относительно точки О в сторону движения часовой стрелки. Силами, препятствующими опрокидыванию, являются G и Р^, направленные относительно точки О в сторону, обратную движению часовой стрелки. Определим опрокидывающий момент: оир = = 45 1 = 45 кн-м. Рис. 78. Определим удерживающий момент: Вес массива, т. е. одного метра длины плотины определяется: G = ha.\, где ha 1 -объем массива. Тогда Му = ЧНа 1 --f-fj/Za = +11,25 0,5 = (39,4а2 +5,6) кн м. Минимальной ширине плотины соответствует коэффициент устойчивости k=\. Тогда будем иметь: 39,4а2 + 5,6 = 45; а=1 м. § 29, Сцепление и трение скольжения Исследованием явления трения впервые занимался Леонардо да Винчи. В конце XVII в. французский физик Амонтон (1663- 1705) обнаружил независимость силы трения от величины поверхности соприкасания тел. Законы трения были сформулированы французским физиком Кзлоном (1736-1806). Если к твердому телу, покоящемуся на шероховатой горизонтальной плоскости (рис. 79а), приложить горизонтальную силу S, то действие этой силы вызовет появление силы сцепления Рси. = - S, представляющей собой силу противодействия плоскости смещению тела. Благодаря сцеплению, тело остается в покое при изменении модуля силы S от нуля до некоторого значения S м Это значит, что модуль силы сце-пления тоже изменяется от Fcu = 0 до F = F в момент начала дви- жения. Модуль максимальной силы сце- Рис. 79а. пления, как показывает опыт, пропорционален нормальному давлению N тела на плоскость. В рассматриваемом случае N~G. сТ=/сц- (29.1) Коэффициент пропорциональности / = -5 является отвлеченным числом и называется коэффициентом сцепления. Коэффициент сцепления зависит от материала и физического состояния соприкасающихся тел и определяется экспериментально. Его величина для материалов, используемых в технике, обычно меньше единицы. Так как максимальное значение силы сцепления равно ДцЛ/, то модуль силы сцепления всегда удовлетворяет условию Fcn<U- (29.2)
Направление силы сцепления противоположно направлению того движения, которое возникло бы под действием приложенных к телу сил при отсутствии сцепления. При скольжении тела по шероховатой Рис. 796. поверхности к нему приложена сила трения скольжения. Направление этой силы, противодействующей скольжению, противоположно направлению скорости тела (рис. 79, б). Модуль силы трения скольжения пропорционален нормальному давлению N: F = fN. (29.3) Коэффициент пропорциональности / называется коэффициентом трения скольжения и определяется опытным путем. Коэффициент трения скольжения является отвлеченной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления. Однако, в элементарных расчетах зависимость коэффициента трения скольжения от скорости и удельного давления часто не учитывается. Экспериментально установлено, что / < /сц- Реакция R реальной (шероховатой) поверхности, в отличие от реакции идеальной (гладкой) поверхности, имеет две составляющие: нормальную реакцию N и силу сцепления Рсц. (или силу трения F при движении тела). Угол фсц, образованный реакцией шероховатой поверхности с нормалью к поверхности в предельном состоянии покоя при F = Ff, называется углом сцепления (рис. 80). Тангенс угла сцепления равен коэффициенту сцепления: или 9cu-=arctg/e . (29.4) Угол, тангенс которого равен коэффициенту трения скольжения, называется углом трения. Угол сцепления можно определить опытным путем. Прибор для определения угла сцепления очень прост. Он представляет собой наклонную плоскость, угол наклона которой а можно изменять (рис. 81, а). Зафиксируем угол наклона а плоскости OA, при котором помещенное на ней тело находится в предельном состоянии покоя и сила сцепления достигает максимального значения. Построим замкнутый треугольник сил, действующих на тело, и определим угол а (рис. 81,6): 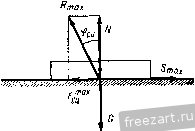 Рис. 80. т. е. угол наклона плоскости а, при котором тело находится в предельном состоянии покоя, равен углу сцепления ф^ц. Величину коэффициента сцепления для соответствующих материалов (тело - плоскость) можно определить по таблице тангенсов углов, так как /сц = *&Фсц- 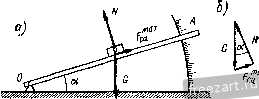 Рис. 81. Конус с вершиной в точке касания тел, образующая которого составляет угол сцепления с нормалью к поверхностям тел, называется конусом сцепления (рис. 82). Поверхность конуса сцепления представляет собой геометрическое место максимальных реакций опорной поверхности. Действительно, максимальная реакция поверхности может занимать различные положения на поверхности этого конуса, зависящие от направления силы S, стремящейся сдвинуть тело (рис, 80). Пространство внутри конуса представляет собой совокупность возможных положений реакций опорной поверхности в состоянии покоя. Пусть к покоящемуся телу приложены силы (й том числе вес тела), линия действия равнодействующей Р которых лежит внутри 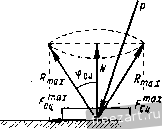 конуса сцепления (рис. 82). Эти силы не приведут тело в движение, так как сила Р будет уравновешена реакцией поверхности. Рассмотрим равновесие сил, действующих на тяжелый брусок, опирающийся на две шероховатые плоскости (рис. 83). В точках А и В возникают реакции опор, линии действия которых не выходят за пределы конусов сцепления. Проведя линии А - I, А - , В - / и В - fV, составляющие углы сцепления ф1ц и фзсц с перпендикулярами к опорным плоскостям, восставленным в точках А и В, получаем границы кону-у^ сов сцепления. Четырехугольник р^ g2 Ытп, образованный этими ли- ниями, внутри которого могут пересекаться линии действия реакций опор Л и В, называется областью равновесия. Брусок АВ находится под действием трех сил: его веса G и двух реакций опор и R. При равновесии линии действия этих трех сил пересекутся в одной точке. Так как любая точка площадки Ытп может являться точкой пересечения линий действия реакций опор Л и В, то брусок находится в состоянии покоя, б если линия действия силы веса бруска пересекает область равновесия. В случае, если линия действия силы веса проходит через точку k области равновесия, брусок находится в предельном состоянии покоя. Брусок не может удержаться в указанном на рисунке положении, если линия действия силы веса проходит вне области равновесия. Если на брусок действует несколько задаваемых сил и они приводятся к равнодействующей силе, установленным условиям должна удовлетворять эта равнодействующая. § 30. Примеры на равновесие сил, приложеиных к твердому телу при наличии сил сцепления Пример 20. Определить величину груза Р, удерживающего тело весом О на шероховатой наклонной плоскости с углом наклона а, который больше угла сцепления ф^ц (рис. 84а). 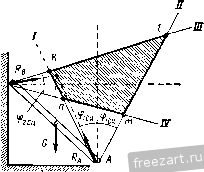 Рис. 83. 1 ... 4 5 6 7 8 9 10 ... 44 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |