

 |
 |
|
Навигация
|
Главная » Мануалы
Таким образом, отличие от рассмотренных н предыдущей задаче вьтужде1шых колебаний, вызванных неуравновещенностью ротора, н данном случае резонанс (ыстунает при любом из двух значе1Шй (X) угловой скорости вращения ротора. Найдем отношение ампл1гтуд вблизи ре.зонанса, соответствуюнтето второму значс1Н1ю критической скорости. Из (6) и.мее.м: Из уравнения (9) следует, что при этих колебаниях ось ротора описывает кротовой конус в направлении, обратном собственному врашегнно ннншделя. Такое движение называется обратной нренессней ротора. Найдем далее отношение амплитуд вблизи рез01ынса, соответствующего первому значению критической скорости. Имеем: b, cl - QU - Ь' )? . /,п1 cl,~ - Лы? ~ cl - QL, ~ > U - AT в этом случае движение оси ротора соответствует прямой прецессии. Итак, если вынужденные колебания вь1зываются силой постоянно(1 по направлению, величина которой меняется с частотой собственного вращения ротора, то возможно появление колебаний двух видов, соответствующих обоим значениям (8) крнпшеской скорости. FTepBLie колебания соответствуют прямой прецессии, а вторые обратной прецессии ротора. 4°. Влияние вязкого трения на вынужденные колебания твердого тела с двумя степенями свободы. Рассмотренная в предыдущем пункте З' теория вынужденных колебаний системы хорошо согласуется с действительностью во всем, за исключением одного результата. Хотя при резонансе и наблюдается Резонанс наступит, когда знаменатель в этих раиенствах обратится AV -(г/ -Q4-Бш -)- = 0. (7) Отсюда находятся два значения критической скорости: (522 устойчивость равновесия и малые движения системы [гл. кт рост амплитуды колебаний, но этот рост никогда не становится неограниченным, как это получалось в двух предыдущих задачах. Объяс11е1ще этога несоответствия кроется в наличии сил сопротивления, которые не учитывались в пункте 3°. Поэтому мы рассмотрим ниже задачу 456, но с добавочным учетом сил сопротивления. Задача 458. В условиях задачи 456 определить вынужденные колебания шпинделя веретена, учитывая силы вязкого тре1щя, которые создают моменты: относителыю оси v равный (--ii i и относителыю I k \ оси Z равный ---rj>i , где k - постоянный коэффициент (характе- \ / ристика трения). Решение. Согласно теореме об пзмснещи. главного момента количеств движе1н1я, имеем: [ Лшр - В\] = (-cl-}-Q j-j 2i - I ii - mweb sin wt, - [Лш-f BP] = ict-Q )y, + -i-.-mweb cos wt. Внося в эти уравнения значения р и находим: Вг, - Awy, -- i, -- (с/ - Q/.j) г, = - mwebl sin wt. By I -]- Aw} kj/x -j- (cP - Qli)yi = - mwebl cos wt. Общее решение этой системы неоднородных линейных дифференциальных ypaBneimfl складывается из общего решения системы бе: правых частей (однородная система уравнений) и частого решения неоднородной системы. Первое решешш определяет затухающие свободные колеба1шя системы н было получено в задаче 455. Второе частное penienne, определяющее вынужденные колебания системы, будем искать в виде: у, = а, cos со/--А, sin со/, г, = 05, sin со/--.j cos со/. (3) Подставим эти 311ачс1шя в уравнения (2). Имеем: - o.2wB sin со/ - bwB cos wt -j- Лсо'а, sin со/ - .46Co cos wt -[--j- kaw cos wt - kb.w sin wt -\- (cl - 04)2 sin wt -f- -f (cl - Q4) U2 cos со/ = - mwebl sin wt, (4) - OiCDB cos wt - bxwB sin wt -\- aAw cos wt - b.Aw sin to/ - - Uikw sin со/ -L bxkw cos со/ -\- (cl- - Q/j,) ai cos wt -\- -) (cf - Q/j) &i sin со/ = - tnwebl cos wt. (5) (14) Сдвиг фазы возмун,ающей силы по отнощению ic вынужде.....,im колебащям определится уравнением tgT== (fi -Л)ш'(с^2 д/) (15) Рассмотрим, какова будет амплитуда колебаний и сдвиг фаз при резонансе, когда (Д-Д) ) -(t/- -Q/2) = 0. (l(j) Из (14) определяем значение амплитуды r, = lwebL (17) Иа (15) находим сдвиг фаз 7 = 0,51:. (18) Приравнивая нулю отдельно члены, содержащие sin (о^ и члены, содержащие cos <ot, находим: - ауВш а,Л(о^ -L bikuy -l а, (сР ~Qk) = - т<х?еЫ, (7) - й^йш - *1 Л ) + М + К (с- - Q) О, (8) - byBiu - йгД' - a,Au) -г 1 (f/ - Q/.) = 0. (9) Из этой системы алгебраических уравнений определяются а by, а. й/. m.oVW (й - Л) - (сЯ - QLM , . - mm-ebluik Прежде чем по этим значениям а а^. 2 найти j/ г, согласно (3), введем для упрощения выкладок новые постоя1Н1ыс р и y, равные р cos Y = (fl -Д)со -(/ -Q/a), psinY = -шА. (12) Тогда, исходя из (3), получим: V, - = - cos (tor - f), Zi=- , - sin((o -r). (13) Следовательно, амплитуда вынужденных колебаний равна 624 J-СТОЙЧИВОСТГ. РЛВ1ГОПГ;СИЯ и МЛЛЫР. ДППЖКНИЯ СИСТР.МЫ (ГЛ. Х!П Таким образом, ири резонансе амплитуда вынужденных колебаний с учетом сил трепия не растет иеограничеппо, а принимает конечное значение. Фаза колебаний отличается от ()азы возмун,а10И1ей силы на 0,5 т:. Найдем, далее, значение амплитуды вынужденных колебаний и сдвига фаз при неогр.тничетюм росте угловой скорости вращении ротора. Из (14) и (15) имеем: TlTTr-Tr; limtg7 = 0. (19) Сопоставляя эти значения с результатами, полученными в задаче 4о6, где вынужденные колебания рассматривались без учета сил сопротивления, видим, что при неогргниче1пюм росте угловой скорости роюра предельные величины амп.тигуды колебаний не отличаю 1ся друг or друга, а сдвиг фаз в обоих случаях стремится к ну.тю. Вда.ти or )е:тонаиса вынужденные колебания с учсто.м сил соп[)от1П!ления мало отличаются от вынужденных колебаний без учета сил вязкого трения. 5. В л и я н и е гироскопических сил на свободные колебания тпердого тела с четырьмя степенями свободы. Для составления дифференциальных уравнений малых колебаний твердого тела при наличии гироскопических сил следует применять теорему о движении центра инерции системы материальных точек вместе с теоремой б пзменетжн главного мо.мента количеств движения системы материальных точек в относптельном движении но отно-шеиню к центру инерции. Согласно первой теореме имеем: Mxir,; My = R;, MSR , (1*) где М - масса твердого тела; л' у^, - координаты центра инерции (тяжести) твердого тела в сис1еме неподвижных осей коорднна!; R , R R - проекции главпо10 вектора внеинньх сил, при;южепных к твердому телу. Вторая теорема приводит к соотнои1е1нтя.м где [..., /. L.,--главные моменты количеств лвиже1И1я относн-телыю осей, движущихся поступа1ельцо вместе с центром инерции п (тяжести) твердого тела; w(F) - главные моменты висшнтгх сил относительно тех же осей. Если осеси.мметричпое твердое тело вращается с большой угловой скоростью (О вокруг си симметрии, которая совпадает при отсутствии .малых колебапип тела с осью х, то с точностью до вели- мин первого порядка малости главные моменты количеств движения относительно осей координат, движущихся поступательно вместе с центром инерции твердого тела, будут; /.= Лео, (3*) где Л - MOMeiTT инерции твердого тела относительно оси симметрии; В - момент инерции твердого тела относительно любой оси, перпендикулярной к оси симметрии и проходящей через центр инерции тела; р - малый угол поворота оси симметрии, отсчитьгваемый от оси X в плоскости ху\ 7 - малый 1утол поворота оси симметрии, отсчитываемый от оси х в плоскости xz. При изучении поперечных колеба1щй обычно пренебрегают малыми продольными перемещениями твердого тела, т. е. полагают координату хс неизме1той. Тогда первое уравне1ше (1*) отпадает. Если, кроме того, рассматривается равномерное вращение твердого тела, 10 отпадает и первое уравнение системы (2*). Для решения задач о свободных колебаниях твердого тела, в которых возможны вышеуказанные допущения, может быть рекомендован следующий порядок действий: 1. Выбираем две системы координат: первую систему - жестко свя-saiHiyio с твердым телом и вторую - неподвижную систему координат. 2. Применяя теорему о движе1ши центра инерции, составляем два дифференциальных уравнения движегшя центра тяжести. 3. Пользуясь теоремой об изменении главного момента количеств движе1шя в относительном двржении по отноп1ению к осям, движущимся поступательно вместе с центром инерции, составляем остальные два ли()фере1щиальных ураштения .малых колебаний твердого тела. 4. Интегрируя полученную систему дифференциальных ура1И1Сний движения твердого тела, находи.м частоты с1Юбод-ных колебаний, г.тавные к'оле-бания ротора и обитее решение задами. Задача 459. Жесткий ротор массы М вращается и двух упругих опорах .4, и В\. Козрффициепты жесткости левой опоры с правой (рис. а). Расстояние между опорам равно /. Центр тяжести С  К задаче 459. 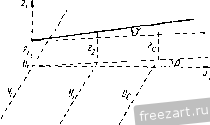 ротора вместе с подипнпткамн находится иа расстоянии /, от опоры А\ и на расстоянии 4 от опоры В\. Ротор вращается вокруг оси симметрии с постоянной угловой скоростью ш. Момент иперции роюра относительно оси симметрии .V/ равен А, отностельно оси, / перпендикулярной к оси вра- щения н проходятцей через центр тяжести ротора, равен В. Найти свободные колебания ротора. Р е щ е и и е. Рассмотрим малые колебания ротора около положения равновесия (равномерного вращения около горизонтальной оси). Неподвижную систему координат xyz выбираем так (рис. б), чтобы ее начало совпало с левой опорой в положении равновесия. Дадим ротору нроизволь-1юе перемещение (рис. б). Координаты левой опоры обозначим Z[, координаты правой опоры jj 2-55, координаты центра тяжести ус, zq. Изменением координат Х|, Xi, хс как величинами более высокого порядка малости будем пренебрегать. Угол между проекцией оси ротора па плоскость ху и осью X назовем Р; угол между осью ротора и ее проекцией на плоскость ху обозначим Y- На рис. в, г ось ротора спроектирована па координатные плоскости ху и XZ. Выразим координаты центра тяжести и углы р, fi через независимые координаты Vi, Zi, у^, z., вполне определяющие положение 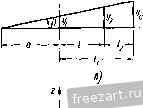
к задаче 450. ротора. Имеем на основании рис. б, в п г: а I / (О § 51 ВЛИЯНИЕ ГИГОСКОПИЧЕСКИХ СИЛ 627 Р=. (3) т. = . (4) На основании теоремы о движении центра инерции можно написать два дифференциальных уравнения: Му(, = - с,у, - Сф, . (о) MZ = - CiZi - CZ, (б) где в правой части стоят проекцин на соответствующие оси упругих реакций пружин. Переходим к составлению дифференциальных уравнений малых колебаний ротора вокруг осей параллельных у, z н проведенных через центр инерции колеблющейся системы. [лавные моменты количеств движения системы с точностью до малых величин первого порядка малости включительно будут: 7.=: Л (О, (7) Л = Л(оЗ-/97, (8) 4=-- Т+-р. (9) Главные моменты внещних сил относительно осей, проведенных через центр инерции, легко находятся из рис. а: L cA9 = СО) V т^, = - z,Ci/ ~ zic,l (11) Пс(Р1)=у^с,/,-у,Суг,. (12) Исноль.зуя теорему об изменении главного момента количеств движения в относительном движении по отнощению к центру инерции и выраже1!ия (8) - (12), имеем Л со - fif = - zc/i - ZyCi/i, (13) Л(07 +/?p:=;/,C24-f JiCi7. (И) Подставляя в уравнения (5), (6), (13), (14) значения у^, z, р, у, получим для нахождения у у, у^, Zf, систему четырех линей1н.1х однородных дифференциальных уравнений: м. (/,3?.j - /у,) + с,/у, + с4у^ = 0, (15) М (Л?. - hz{) + cylzy + c4z =0, (16) Л (О (j>, - J),) - (2 - г,) -f c44z. -f cylxlz, =0, (17) A Ш (i, - i.) £ (j/, p,) - - cyhlyy = 0. (18) yi=Lh sin (pt-]-a), z, = L\ cos (pt -f a), Zi = Dl cos (pt -\- a), (19) где Du Di, D3, Di, p, a - постоянные, которые должш,1 быть определены так, чтобы (19) удо[1летворяло системе диффере1щиалып.1х уравнений (15) - (18), Внося (19) в (15) - (18), имеем, после сокра-шения соответственно па s\n(pt-\-a) и cos(/)/4-a) и приведения подобных членов, однородную систему четырех алгебраических уравнений относительно Dj, D, D, Di. (Cyl - \- Mlip-) Dl -\- (Cil - Mlip) D.2 = 0, (c,/-f AUiP) Da Ч- i<-J - Mlip) Di = 0, - AwpDi -\-AwpDi-{-(cilxl~Bp)D3-\-(€il:,l-\-Dp) D4 = 0, (Bp - cilyl) Dl - (Bp -1- c.j/ /) Di + AwpD-, - AwpDi = 0. (20) Легко показать, что система (20) распадается на две. Действительно, складывая и вычитая первые два и последние два уравнения, получаем: (cil-\-Ml.,г) (Dl -i- D3) + - Mhr) (Di-Dd = 0, (cil -L Mli f) (Dl ~ D3) -f (Cil - Mtip) (Di - Д) == 0, (Пр + Awp - cilil) (Dl -1- Da) - (Bp + Awp -V Cil/) (Di + Dd = 0, (Bpi Amp - cilil) (Dl - D3) - (V - Awp + Cilil) (Di - D,) = 0. Группируя уравнения, имеем систему для нахожде1ШЯ D.-j-Dj и Di-\-Di: (Cil + Mlip) (Dl + Da) + Ы - {Di + D4) = 0, (Bp- + Лео/. - cilil) (Dl -f Da) ~ (Bp + Л со/. + 6-,/) (Di + D4) = 0, и систему для нахождения Di - D3 и D,i - D4: (Cil -Ь уИ/,/:;0 (1 - Дз) + (с^ - Mlip ) (Di - D4) = О, (Bp - ЛоФ - Cl ,) (D, - Da) - - (Bp - Лш;; 4- Cil.il) (Da - D4) = 0. (21) Частное решение этой системы будем искать в виде y\ = L\ sin {pta), ПЛНЯНИЕ ГИРОСКОПИЧЕСКИХ СИЛ Прираппипая определители систем (21) и (22) пулю, получаем laa частот1П.1Х ураипспия *): {Bp -i- До.; - cl ~ с,1\) {с, -i- с, - Мр) -f -г iif = О (23) {Bp -Ашр- c,li - r,/f) {с, -р с, - Мр-) -г- {с,/у -1- Ы,) = 0. (24) Докажем, что уравиепия (23) и (24) не имеют общих корней. Предположим, что оби|,ий корень /?, существует. Тогда при p = Pi оба уравнения удовлетворяются одповремеьню. Вычитяя из nep :oio уравнения второе, получаем: 2/l(o/j,(c,-!-r,2 -ЛI/i) = 0, т. е. общими корнями могли бы быть г = 0 и .,= /р. но оба эти значения не удовлетворяют исходным уравнениям. Покажем теперь, что Koptm частотн[>1Х уравнений вещественны. Для этого рассмотрим 4ункции /, {р) = {Bp -]-Ашр - c,ri - cJ.I) (с, с, - Мр) - \- {Су!у c,lif, (2о) /, {р) = {Bp - Ащу - cl - г,/[) (г, 4- г, - ЛУ) + (с,/, + clf (26) и найдем пх зпачегпм для некоторых характерных значений аргумента р:
Но существ), опмса/Тиая операция означает разложение иа мпожк-тс.ти частотного ураинс1Н|я системы (20). 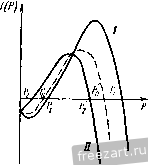 Из таблицы видно, чю непрерыв!1ые функции f\{p) и /{р) при изменении аргумента р -оо до -[-оо четыре раза меняют знак. Вспоминая, что (23) и (24) являются уравнениями четвертой степени, можно утверждать, что каждое из уравнений (23) и (24) имеет по два отрицательных и два положительных корня, т. е. корпи обоих уравнений вещественны. Отметим, что рассматриваемые корни обладают интересным свойством: отрицательные корпи одного уравнения равны по абсолютной величине положительным корням другого, и наоборот. При угловой скорости 10, равной нулю, уравнения (23) и (24) совпадают и принимают вид (Bp-c,l\-cir\)(c, -- -уИ/)Н- -1- (,V,-}-c,/,) = 0. (27) Корни уравнения (27) определяют частоты свободных колебаний невращающе-гося ротора. На рис. д представлены i) графики функций /,(/?), /{р) и f(p), К задаче 4.59. причем через /о(я) обозначена левая часта (27). Как видно из графика положительные корни этих уравнений, т. е. частоты свободных колебаний рогора, располагаются в следующем порядке: ;i</o<>i<;i<,Oo<,oi- (28) Здесь рй, pis - частоть! свободных колебаний невращающегося ротора. Из уравнений (21) и (22) видно, что для корней первого частотного \равнения частное решение будет иметь вид j/, = D, sin ipi --а), ~ i = Dl cos ipt -j- a), yi = DiSm (pt-+(x), Zi-D-i cos {pt a), так как система (22) в этом случае имеет только травиальное реще1же - Дз = 0 и Di - 7)4 = 0. Аналогично для корней второго частотного уравнения получаем: yi=Di sin(;pH-a). 2i=-D, COS {pt-o), yi = Di sin {pt + a), Zi = - Di cos {pt a). (29) 1 ... 59 60 61 62 63 64 65 66 |
||||||||||||||||||||||||||||||||||||||
 |
 |