

 |
 |
|
Навигация
|
Главная » Мануалы Легко проверить, чго вследствие указанной выше особенности корней частотных уравнений можно ограничиться подстановкой в (29) и (30) лишь положительных корней соответствующих частот1н.[Х уравнений, ибо отрицательные корни не приведут к новым линейно независимым частотным решениям. В итоге корням pi и р[ отвечают первое и второе главные колебания, при которых ось ротора описывает круговой конус, вращаясь в том же направлении, что и ротор. Эти движения называются прямой прецессией ротора. При <:прямой прецессии вектор угловой скорости твердого тела (при вращении вокруг оси симметрии) и вектор угловой скорости оси ротора образуют острый угол. Корням Pi и pj, отвечают третье и четвертое главные колебания, при которых ось ротора описывает круговой конус, вращаясь в направлении, обратном вращению ротора. Эти движения называются обратной прецессией ро-юра. При обратной прецессии вектор угловой скорости твердого тела (при враще1ши вокруг оси симметрии) и вектор угловой скорости оси ротора образуют тупой угол. Таким образом, свободные колебания ротора складываются пз четырех гармонических колебаний, два из которых соответствуют сии и два обратной . Подчеркнем, что частоты свободных колеба1Шй вращающегося роюра, как видно из уравне1шй (23) и (24), зависят от его угловой скорости. Заметим еще, чю задача peniena для горизо1Ггалы10го ротора, цепгр тяжести ротора лежит вне участка между опорами. Если же центр тяжести ротора лежит между опорами (рис. с), то во всех уравнениях надо измешгть знак перед 4 на противоположный. Ь'\ Влияние гироскопических сил на вынужденные колебания твердого тела с четырьмя степенями свободы. Самоцентрирование. При составлении дифференциальных уравне1Н1й малых движений твердого тела можно применить теорему о движении центра инерции системы материальных точек и теорему об изменении главного момента количеств движения системы материальных точек в относительном движении по отношению к центру инерции. Указанные теоремы используются в форме пункта 5° настоящего параграфа (уравнения (1*), (2*), (3*)). К задаче 459. прямой прецёс- 632 устойчипость рлвиовесия и малые движения СИСТЕЛ1Ы [гл. XMI Ди([)ференииальные уравнения вынужденных колебаний отличаются от рассмотренных в нугнсте 5° этого параграфа уравнений свободных колебаний наличием в правых частях возмущающих сил и их моментов. К весьма распространенной в технике категории возмущающих сил относятся силы, вызванные статической и динамической неуравновешенностью роторов. Статическая неуранновегпенность обусловливается смещением центра инерции ротора or геометрической оси враще1щя. Динамическая неуравповешентюсть является следствием наклона главной оси тшерции твердого тела по отношению к геометрической оси вра-и|,с1шя. ГГ р и р е И1 е и и и задач на определение вынужденных колебаний твердого тела с четырьмя степенями свободы рекомендуется следующая последователь-н о с I ь действий: 1) выбираем обобщешиле координаты; 2) пользуясь теоремой о движении центра инерции, составляем два диф(})ере1щиалыц.1х уравнегшя движения центра инерции твердого тела; 3) составляем выражетшя главного момента количестп движения сис1емы в от1Юсителы10м движении по втпошепию к центру инершш и выражение глав1Юго момента нненпшх сил относительно осей, дви-жуитихся поступательно вместе с центром инерции твердого тела; 4) ноль.зуясь теоремой об изменении глашюго момента количеств движения в относительном движетши по отношению к центру инерции, выписываем еще два диффере1щиальных уравнетшя малых коле-баттй; Г)) находим частное решение неоднородной системы диф(})ерен-циальных уравнений, определяющее вынужденные колебания. Задача 460*). Горизонтальный жесткий ротор массы М вращается с постоянной угловой скоростью О) в двух упругих опорах и Bi. Опоры перемещаются в од1юродном упругом поле. Коэффициенты жесткости опор: левой с правой с^,. Расстоя1ще между опорами /. Расстояние от центра тяжести ротора С до опоры Л, рав1Ю / до опоры Bi рав1Ю Далее, Л - момент иперции ротора относительно оси симметрии, В-момент инерции роюра от1Юсителыю оси, перпендикулярной к оси вращения и проходящей через его центр. Определить вынужденные колебания ротора, вызванные его статической и динамической неуравновешенностью, если центр тяжести ротора отстоит от 1еомстричсской оси на расстояние е, а главная ось инерции ротора, близкая к геометрической оси, обра- *) Л. С. К с л ь 3 о н. Самоцентрирование и уравмовешивапие жесткого ротора, вращающегося в днух упругих опорах. Доклады АН СССР, т. 110, вып. 1, 1956. г^, = г -е sin 0) j Обозначим через 3 угол между проекцией главной центральной оси на плоскость ху и осью х. Угол между проекцией геометрической оси на Плоскость ху и осью х обозначим S.j. Эти уг.ты связащл сботпо- p = fi-LScosH-s), (3) где (со - е) - угол между п.юскостью, в которой лежит утол 5 и плоскостью ху. Обозначая аналогично через \ угол между проекцией главной центральной оси инерции па п.чоскость xz и осью х, и утол между проекцией гео,метрической оси па п,тоскость xz и осью х, находим: 7 = 7-2 -- 3 sin {Ы - £). (4) Подставляя найденные значе1Н1я у^., z. В, 7 в дифференциальные уравнения движения ротора (1), имеем: Щ ~\~ \У\ 4 Уг ~ Л'-ч) cos uit, Mz ~ CiZy -j- Co22= Жеш- sin mt, Л 103-7.2- c,/2,j-i-Ci/, = -(Л - Л) ш'Ь sin (coC - t), Aw-i f Др2 - ciLy.~ cjji = {B- A)чуЬ cos (urf - i). Правые части этих уравнений представляют возмущающие факторы, вызиа1тые статической и динамической неуравновещенностью ротора. .чует с последней угол 3. Плоскости, проведенные через геометрическую ось и центр тяжести, а также через геометрическую ось н главную ось инерции, образуют двугранный угол, равный s. Найти также закон вынужденного движения ротора и определить предельные значения коорд1И1ат центра тяжести ротора н угла отк.Ю-нения главной оси инерции от геометрической оси ротора при не-ограничешюм увеличении угловой скорости ротора. Feinenne. Будем исходить из дифференциальных уравпений двнже1П1Я ротора, полученных в предыдущей задаче: А1Ур = -ciyi~c..y.2. Мг = - CyZ, - coj. ЛшЗ - 7 = - ZticJi - ZiCi/y, Если обозначить через у, z координаты точки геометрической оси ротора, лежащей на перссечеппн этой осп с плоскостью, перпендикулярной к оси враньения и проходящей через центр тяжес1и ротора, то координаты центра тяжести будут: у^ =у е cos vat, Используя установленные в предыдущей задаче соотношения 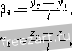 -У^Т^Уч-/. (fi) и систему уравнений (о), находим: М (lipi - IJd + cjyi + с^/уа = Ме/ш - cos ./, М (/ji o - ZjZi) -- Ci/г, -j- = Melm sin ш/, /I {S>i - Ji) - В (-i - 3i) -1- с,/.,/г, ciljzi = = - {B~A) co/S sin ((0/ - s), Ли. (i, - i,) -j- Д G-j - jl) - <iV;2 - lA/yi = = {B - A) ujVS cos ( )/ - £). Полученная система линейных, неоднородных дифференциальных урав-!1ений с постоянными коэффициентами описывает малые колебания ротора, вызванные статической и динамической неуравповешетюстью. PcnieiHie этой системы складывается из общего решешш системьг без npanoil части и частного решения полной системы. Обнсее решешш системы без правой части найдено в предыдущей задаче, - оно отвечает свободным колебаниям ротор,!. Частое рещение полной системы, которое будем искать в виде У| =а, cos ш/ -\- sin со/, = а, sin ш/ -- cos ш/, у.2 = flj cos wt -\- by sin wt, гз = 4 sin wt -\- bi cos wt, определяет искомые щ.щужденные колебания. Для T0IO чтобы найти значения постоянных а,-, Ь^, подставим ре-пиние (8) в уравнения движения (7). Так как эти уравнения должны быгь удовлетворены в произвольный момент времени, то необходимо 1)азделы10 приравнять нулю сумму всех членов, содержащих множителем cos wt, и сумму всех членов, содержащих множителем sin wt. Ii итоге получаем две системы алгебраических уравнений: Жсо- (7.а, - /,аз) 4- с,/а, -\- cja-i = Alelw\ Mw {la-i - liuf) -j- Cila -j- cjui = Melw, - Лео' (дз - ai) -f- Bw - a.i) -[- Ciklai -- cJiluj, = = - (Z? - Л) Ibw cos e. Aw - a) - Bw (03 - fl,) - с аз - Ci7,/ai = = (B - Л) /Sto cos г 5[ иЛИЯПИЕ ГИРОСКОПИЧР.СКИХ СИЛ 633 и /Иш ~~ /,йз) -i- c,lb, + с/Аз = о, Мч {1ф.г - 1А) - с,/Л.2 -;- cjbi = О, (й., - й,) \-Bwibi - Л.) -- tsVi f, A.2 = Л оУ {64 - - hi) - \ - Bui Oh - b,) -f f-Ai/i -I- f = = - (Д-Л)8/(0- sin £. (10) И.Ч этих двух систем могут бытв иайдепы значения всех восьми постоянных й|, й^, a,j, а^, h й А так, чтобы частное решение удовлетворяло исходной системе дифференциальных уравнений. Проще всего эти постоянные определяются, если сложить и вычесть первые два и последние два уравнения каждой системы. Тогда из первой системы имеем: {Mkiii - \~ cJ) (а, - ui) - (.4]/, . - с./) (аз - а,) = 0, (II) \{В Л) -1, , 1 (а, - а,) -\{В -I- Л) (0- -l ia, ~а,) = 0, (12) (ЖЛю^ - L с,/) (й, а.) - (.ШУ - Са/) (а, -j- а^) = ЧМе1иу\ (13) \{В - Л) - с, ,1 (oi -г а,) - [(/ - Л) ш' -I Ык\[а, ~\- а,) = = 2(fi-Л)/5ш'cos £. (14) Аналогично из второй системы находим: (/M/ii(o -- с,/) {bl -- b,i) - (/М/,.0 - г./) (Лз - hi) = 0, (15) 1( - А) - {by - й.,) - ( - Л) с..- ; - г,/,/ (й, - ьо = = 2(/5-Л)/8(,>Ч1и S, (16) {Miy -\- с,1) {hi -I - b,) - (/И/,со - с../) {Ь, -j- Ai) = 0, (17) (Л - Л) - с,/7,1 {hi + А.,) - (,В-1- А) w ~ {Ь,-\- Ь,) = 0. (18) Рассмотрим совместно урапнения (11), (12), (17), (18), представляю-шие по существу две группы однородных уравнеш1й, относительно гумм и разностей искомых величин. Если /, (.0) = [{В -I - Л) ш' Н- л/АЛ (Л1/.,о,2.!- - - i(Д Н- Л) - - , ,] (.4J/,o) - с,1) 7 О, (1 fl) то эти системы однородных алгебраических уравнений имеют только тривиальное решение а, = а„ A. = -A j 03 = 4; йз = -А,. J (21) Подставив найденные змачент'я искомых постоян1Нлх в оставшиеся уравнения (13), (14), (15), (16), получаем: (М/ш' с,/) а, - (/И/,ш^ - с il) аз = Ме1ш\ (/? - Л) ш' - f, ,] а, - (В - Л) (0 с,/,/] аз = = (В-Л)Ш-С05£, (Ж/,ш' -f f,/) - (Miy - f,/) = О, [(/? - Л) ш' - с, ,] - [(Я - Л) (0 -\- c,/,/J = = (/5 - Л)8/ш- sin £. у Теперь легко находятся все искомые величины. Если, кроме того, Л С' ) = ((й - Л) со- + (Ж4ш' ,/) - - - [(В - Л) ш' - с, ,] (,И/,о/ - г,/) г£ О, (22) то постоянные будут равш,! /ТТ 1 - -г /-Л - - (;И/,и. -f.j/)(B-Л) (о2 COS £}, (23) а;, = - {МеЬ^- [(В - Л) со- - c,/,/J - - (yW/.,co-(-f,/)(fi -Л)/ош- cos с}, (24) = - (.M/,co- - с/) (В - Л) /2(0- Sin £, (20) ;,= - j(MliW--Ctl)(B~ Л)/5ш^sin г. (26) Вводя вместо постон1шых я я.2, Од, ai, bi, b., / ; /74 новые постоянные г), г^, 1 связанные с ihtmh соотношениями: а, = а.д = л, cos/, = - i.2 = rSin/, аз - ai= г., cos <\), Ьз - - bi - r. sin ф, nepeiinuieM уравнения (8) в виде j;, = r, COS((0/ -Х), г, = г, sin((o/ -х), J.2=r.2 COS((0/- ф), 2o=r.2Sin(co/- (jj). Па основаштн ура1шений (28) заключаем, что выну;т<денные колебания ротора, вызванные его статической и динамической неуравно-вешеиностью, представляют прямую прецессию с угловой скоростью j, равгюй угловой скорости ротора. (27) (28) Заметим, что статическая и динамическая неуравновешенность в данноН системе не могут вызвать вынужденных колебаний, соответ-ствуюнтих обратной прецессии ротора. Найдем теперь предельные значения постоянных, определяемых равенствами (23) - (26) при пеогра1Шче1П10м возрастании угловой скорости: lim а, = 7, 8 cos в -е, lim ат = /.2 8 cos е - е, lim А, = / 8 sin е, ш -► оо lini b = i<l,Ь sin s. (29) Внося предельные значения постоянных в уравнения (8), находим выражения координат при w = oy. (30)
Для определения предельных значений координат центра тяжести ротора и угла отклонения его главной оси инерции от геометрической оси ротора, подставим предельные значения координат (30) в уравнения (2), (3), (4). Используем зависимости (6). В итоге получаем: lim у^ = 0, со -+ СО lim (5 = 0, lim (=0. (31) Следовательно, при неотра1ШчеШ10м увеличении угловой скорости вращения неуравновешенный статически и динамически ротор стремится совместить ось вращс|щя с главной центральной осью инерции. При неограниченном увеличении угловой скорости, жесткий ротор, врашаюнтийся в двух упругих опорах, располагается так, что устраняется его статическая и динамическая неуравновепшнности. Ротор с четырьмя степенями свободы (не считая вращения вокруг оси) обладает замечательным свойством самоцентрирования. Это свойство находит широкое применение при конструировагши современных высокооборотных машин. Задача 461. В условиях предыдущей задачи определить критические угловые скорости рогора (при отсутствии сил трения). Критическими называются значения угловых скоростей ротора, при которых ампли1уды вынужденных колебаний неограниченно возрастают. Ре Hie ни е. Как следует из уравнений (8) предыдуи,ей задачи, координаты точек ротора неограниченно возрастают одновре.менио с коэффициентами а,-, bf. Из равенств (23) - (26) видно, что это будет при fi ( >) = [( - А) 4- сАП {М1.У' -Ь cil) - - \{В - Л) (0 - cilli] (Miy- - cj) = 0. (1) Представим функцию /9(10) в виде /, (ш) = (z? - Л) [с, + с, - ТИш^] ~f /И/ш^ (c,/f + СоД) - сус./ (2) и исследуем ее. Для этого для значений со, равных: О, / оо, находим значения /(ш). При этом следует различать два случая: В>Л и Л>В. Результаты вычислений сведем в таблицу:
Из таблицы видно (см. стр.629), что при /?Л уравнение (I) имеет два положительных вещественных корня toi и щ, т. е., что резонанс наступает при этих двух значениях угловоИ скорости ротора. В этом случае имеется два значения критической угловой скорости, причем Во втором случае, при А' В, уравнение (I) имеет один положительный вещественный корень и) т. е. у ротора одна критическая угловая скорость, причем (Oj < l/ * Упомянутые критические угловые скорости жесткого ротора в двух упругих опорах определяются как корнн биквадратного урав- S 51 ВЛИЯНИЕ ГИРОСКОПИЧЕСКИХ СИЛ 63fl нения (l): 2М {В - А) где Ri = (1 -1- с.) (В - Л) + м(с,1= -;- с,/-:) 5, = (1 + с,) (В - Л) - ж (fЧ- с,0 При Л = 0 формула (3) дает значение критической угловой скорости без учета гироскопического эффекта. До сих пор при определе1П1И вынужденных колебаний ротора мы предполагали, что /, (ш) 0. Рассмотрим теперь особый случай, когда Л(ш) = а (4) Найдем разность Л Н - Л (со) = 2 Л (с, + С2 - УИ.о^). (5) Из (5) следует, что при условии (4), функция /Д(о) не обраисается в нуль, если с, -- 2 - УИш^ и ш r?i- 0. Найденные н иред[,1лу[цей задаче значения й,-, й,- и при услОЕиш (4) удовлетпорярот исходным дифференциальным уравнениям движения. Значит, в этом случае мы имеем те же резонансные колебания и критические угловые скорости, которые уже определены уравнением (3). На этом основании можно заключить, что при во.злействии на ротор возмущающих сил, вызиз1и1ых его статической и динамической неуратюнещениостью, резонатстых колебаний, соответствуюнщх обращению в нуль, функции /((со) возникнуть не могут. Однако при действии других возмун1ающих сил, изменяющихся с частотой, равной угловой скорости ротора ш, резонансные колебания, соответствуюи1ие обращению в нуль/j (w), могут возникнуть. Доказательство этого утверждещш приводится в следующей задаче. Задача 462. В условиях задачи 460 определить крити'1еские угловые скорости ротора, если возмущаюпия сила равна F= cos wt. Возмущающая сила с постоянной амплитудой приложена в центре тяжести ротора и сохраняет неизменное направление, параллельное оси у. Рещение. Дпф()еренцнальные уравнения движения ротора будут (см. уравнения (5), (6), (13), (14) задачи 459): Ус + i-i + = F< cos Mt, M5.-bc,,--C29=0, Лшр - 7 + ciZ 4- cjyz, = 0, Л(07 -f- - ciyi - Cy/iyi = 0. УСТОЙЧИПОСП. РЛВН01ЕС11Я и МЛЛЫЕ ДВИЖЕНИЯ СИСТЕЛ\Ы ГЛ. XMI Подставляя выражения для у^, z, 3, у (см. уравнения (1) -(4) задачи 459) в эти уравнения, находим: М- г,у^) --- с,/Jl - - clyi = /-о / cos ш/, М (/, ., - / г,) -г /-ч - ./г.. = О, Аш(у^ ->i) - (Ь - : ,)-1 - с. г.2 - с,/,/г, = О, Лш (i, - i,) - Л (v., - j},) c,/,/j, - c,Z,/j., = 0. PcHicHHe этой системы линейных неоднородных дифференциальных уравнений с посгоянньпш коэффициентами складьшается из общего решения системы без правой части и частного реишния полной системы.  К - да1С 162. Обитее решение системы без правой части уже найдено, - это уравне1ше свободных колебаний ротора (см. задачу 459). Частное решение полной системы, опрсделяющ,ее вынужден1няе колебания ротора, бу.тем искать в виде 1;, = а, cos 1о/; г, = До sin со/; ) \ (3) J.) = а.т cos О)/; г.2 = Я', sin (о/, J Подставляя (3) в лпс{14)оренциальные уравнения движения (2) и сокращая соответствешю на sin ш/ или cos ш/, получаем систему алгебраических уравнений для опрелс.тения постоянных й а. а- а^. (с,/4- М1ш') а, (с.,/ - М1,ю') а, = F,l, (Г[/-1- /И/.2со) я.. -! - (Ы - /и/ico-) а, = О, Л - Дсо^Д;, - (с,/,/ - /?ш^) -- (с /./ -L /?ш-2) = О, Л uj-ui - Л ш^я.2 - (с,/i/ - fio)-) uj - (сs,/.,/ -i- /ш') a, = 0. 1 ... 60 61 62 63 64 65 66 |
 |
 |