

 |
 |
|
Навигация
|
Главная » Мануалы 5 г>1 плн'лилг. гнрпскопимР-Ских сил 641 Складывая и вычитая первые два и последние два уравнения, находим: (с,/ (а, ~ - а,) {Ы- /И/,со) (из Ч - ад) = [(В-A) i-r:l/l/l(a,-Ua,) - [(Z? - А) + с,4/ (аз -г- аО = О, (г1/-гЛГАУ) (ai -дз)-!- + (с/ - AiW) (а, ~ а,) = F,l, [(/?Л)оз--с,/,/1(а,-а,)- - I (/? А) ш' (аз - а,) = 0. Из эгнх урампепиМ получаем:
формулы (6) показ1.П1Я10т, что а a.i, д. а^ нсогряни.1енпо возрастают, когда /i (w) прибли-жается к нулю. Ири региСнии нрсдыдутсН зд.тачи было з'станов.чено, что / (ш) и /(lu) не имек1т обишх корней. Следопательно, когда /[ (со)-> О, то /2(01) принимает отличное от нуля зна.епис. Поэтому ири мллых /, (ш) первые слагаемые в формулах (0) пренебрежимо малы по сравнению со вторыми. Следовательно, д.чя приближенного определения постоянных можно в (6) отбросить первые части. Тогда а.-=-а., I (7) 642 vcTOiimnoCTi) рлппоппсия и малые движения Системы 1гл. xih Поэтому уравнения движения точек ротора, совпадающих с центрами нижней и верхней онор, будут имегь вид: j/[ = а, cos uif, У> = 0:i cos uit, 2-,=-a. Sin со/, z.2 = - Q;, sin со/. Из ypaRHCHHif (8) вндж), что характер колебаний, вккявасмых силой F вблизи ре;юнанса при соответствующей критической yi\iOBOii скорости. Определяемой и;1 уравнения /, ((о) = 0, отвечает синхронно!! обратной прецессии ротора. Значения критических уг.товых скоростей обратной; нрсцесснн находятся из уравнения (см. задачу 4(50) /, (со) = 1(В - А)ш' -i- c.JU)\ (Л'1/.V -1- с,/) - - (В -А) ш'- - с, , I (.М/,.и^ - г,/) = О, (9) R,=[с, -]- с.,) (Л Л) /И (г,/-; р .,/) >-2 = -; - -i) (/i :- Л) -1- /И (с,/,- L npHicM эти ;щачения всегда вентественны. Таким образом, при действии возмущающей си.ч,1 постоянного направления, изменяющейся по сипус()ида.т|.)и)му ;1акоиу с частотой, равной уг.товой скорости ротора, существуют чегыре и.ти три криги-ческне утловые скорости ротора (в зависимости от соотношения мо-.мснтов инерции А и В). Т'. В ы н у ж д с п н Г.1 е ко.тебания твердого тела при резонансе. /1ис1)фере1нша;и>ные уравпеиия движения твердого тела составляются в соответствии с общими прави.тами, указанными в 4 и Г), пунктах 3 , fi настоящей г.тавы. При рен1епин задач на определение вынужденных Ko.Teoannit твердого тела при р е ;п) и а и с с р с к о-м е п д у с т с я следу ю щ а я и о с л с д о в а г е л к и о с т ь д с й с т в п й: 1) выбираем обобщсппые координаты; 2) ноль;1уяск уравнения.ми Лагранжа и.ти общими теоремами динамики, составляем дифференниалвтис уравнения движения твердого те.та; 3) рассматривая задачу о свободных колебаниях тела, находим частоты свободных кoлeбaниf (резонанснкю частоты); 4) для с.тучая резонанса 1аходим частное pememie неоднородной системы дифференциал!.пых уравненнй движения и накладывая на пего общее pemeime однородной системы, получаем искомое общее решение задачи. Задача 463. Определить пынуж.тен1Н,1е колебашш ншинделя веретена, закреплешюго шарнирно в точке О и имеющего в точке Л плияииг. ГИРОСКОПИЧЕСКИХ сил J. упругую опору с K04(jj([)nunenT0Nr жесгкости с, в любом горизонтальном папраплепип. Центр тяжести шпинделя находится к точке С Угловая скорость BpuuieiiHH ппжплеля ш вокруг осп симметрии постоянная но вели- Р чине. Главные моменты инернии гипинделя относительно осей, проведенных через неподвижную точку О, соответственно paBin.i: осевой MOMCITT ннерцин Л, момент инерции относительно любой оси, перпендикулярной оси симметрии В. Расстояния 0Л = 1, ЛС = А, ОС=Ц. Иа высоте h над неподвижной точкой О, на расстоянии е От оси Симметрии, находится не-уравновешеггная малая масса т ([)ис. к задаче 463). Ввиду малости массы т и расстожшя е пренебречь ее влия1Н1ем на положение центра тяжести и моменты инерцни. Определить вынужденшле колебания иншнделя при резонансе. Р е ш с п н е. Воспользуемся некоторыми резу.тьтатами, полученными ири решении задачи 456, когда для этого же шпинделя были определены выну-жден1п.1С колебания прп значениях угловой скорости вращения, отлич-1И.1Х от pesonanciHiix. Ди11()ере1ншалЫ1ые уравнения движс1и1я имели вид Bz, - Лшу, -\-{с,Р - QLi)2, = - im-hel sin ш/, /Зу, -L Лuji, ~[- (dP - QU)yi = - Dmbel cos (of.  К аадамс 4c3. где у|, г, - координаты точки ишинделя, соприкасающейся с нижней опорой. Частное решение систе.мы, определяющее вынужденные ко.[еба1И1Я, дается формулами тю-bol , J/, = ~---7 -j-y--COS WT, 01- Л),о-: - (cJ -Ql. iiiiii-bd Sin u)/. Это решение удовлетворяет системе дифференциа.мьных уравнений движения при всех значениях угловой скорости вращения ипшнде.тя, кроме кр1тгического (резонансного), равного У В-А' для которого знаменатель в (2) обраитается в нуль. 21 yCTOilIKnoCTh РЛПИОВЕСИЯ и МЛЛЫЕ ДВИЖЕНИЯ СИСТЕМЫ [ГЛ. ХП1 Из ypaBHeimit (2) следуег, что при В1,п1ужденных колебаниях точка с координатами у^, г, будет описыват!, окружность радиусом с угловой скоростью, равной по величине углопо11 скорости вранге-ния шпинделя вокруг оси снуметрии. При этом угол межу1.у направлениями угловых ско[)остей меньше ~ 2. Следователыю, выпуждешн.км колебаниям нншнделя, вызванным неуравновен1еннос1ыо, соответствует прямая прецессия его оси с угловой ско[)Остьк), раыюй ио модулю угловой скорости в[)ашения шпинделя. При вынужденных колебаниях, вызва1шых неуравновешенносью шпинделя, резонансные колеба1Н1я, соотвегствуюинге второму значению критической скорости в возникнуть не могут. Перейдем к онределснню закона вьшуждешнлх колебаний ншинделя при резонансе, когда уг.товая скоросгь шнину|,еля равна кри1нче-ской. Тогда частное решение cиcтeи.l ди([)фе1)енцналы1ых ypainiennii (!) вследствие ее структуры с.тедуег искать в виде у, tdy sin О)/, I г, =г /, cos ш/. / (ti) Вычисляя первую и вторую производные ог у, и Zi по премеш!, подставляем полученные выражения в систему (1) I- 2B/(j(i. - Лшй',] sin ш(- I- ть.ш' - iAd.m -\-{ciP - Q!i)>lh] cos wt - - тшЧ)с1 sm wi, 12flf/,(u-l- Лш )! cos ./ ;-1 - - iBdyW- - tAh,i>r -L -f- (c,/- - Q/.>) 1 sin ш/ = - тч?Ье1 cos lu/. Так как эти рявепства должны быть справедливы в любой wo-МС1ГГ времени, то гюобходимо приравнять коэффициенты при sin Ы, cos cof, f sin mf и f cos со/ в правой и лево11 частях. В результате получаем четыре у|)авнения для определения двух неизвестных: - 2/i<o/; - Awdi = - mw-hel, - lUlu - Л - (г,/- - Q/.,) /I, - О, 2/wd, -- Лш/?, = - inw-bcl, - Bwdi - Awhi -;- (с,/ - Q/.j)dl = 0. s С) vCTOfiiimocrb движения 64Г) Особенность системы состоит в том, что реиюиис первых двух уравнениМ тождественно удовлетворяет оста.тьгн.ш. Иоэюму , , uuhel шЬо/ - / с,1- - (JL, = - = у . (9) Следовательно, уравнения вьн|уждснных колебаним нижнего копна ПНП1НДСЛЯ при реяонансе будут: ~ - I---2 - t ;os int. Из этих уравпсннй следует, что при ре:юпансе вьн1уждсппым колебаниям соответствует -обратная прецессия осп ннншделя. Если угловая скорость гипинтеля меньи1е критнческ'оИ (Л), то, как видно из ypaiHiCHHil (2), знаменатель в иравь1х чаС1ях отрнцате.тен. Таким образом, ось Н1пинделя совсрпьает п1)ямук' прецессию. При резонансе возникают пар;1стаю1цие колебания, соответствующие -o6p;ri-HO(i прецессии оси ппнныеля. Далее, с ростом угловой скорости нн1ипделя зпамснате.ть в уравнениях (2) становится ио,то:Кительным и, таким образом, после резонанса ВЕЮВь возтпсают колебания, соотпетстиуюише чфя.мой нрецесспн шпиндс.тя. § 6. Устойчивость движения 1. И р я лг о М .метол нес л с д о н а н н я. Д,тя нзучерщя устойчивости движения систе\н.1 матери,ьтьиых точек запишем систему дифференциальных уравнений движения в виде системы первого порядка ~ = У. 0-1, Уъ .... Уп< О (Л = 1, 2, ... ,2 ), (1 *) где - обобитенные координаты или oOoOnieinnJe ckojiocth систе-ЛН.1, явля10Н1иеся фyпкцияпl иреме1И1 1. Если J.=/i(0, У-2 = /-г(<1-..)п = /п(П СГ) является мастным рсшеиисм cncieMi.i (1*), соответсгвуюншм заданным нача;н>ным условиям дв1гжс[Н1я: v,=Jio. ,V.2=,V.20. .... J = v o при = 0, (3*) то решение (2-) определяет нетозмущеЕпюе дв[гжсиие системы. Невозмущеппос движение (нстемы назьн!ается устойчивым, если при мало.м изменении начальных условий решения системы (2*) переходят в ропюпия, мало отличающиеся от исход1п.1Х д.1Я сколь угодно больших зпачепиМ /. Такое пснозмуп,еипое движение !1азыцают также движением устойчивым в малом. Если отклонения от невозчушенного движе1шя, кроме roio, при неогра!1Иченном позрастапни времени стремятся к нулю, то такое не-возмуи,енное дпиже1!ие называется асимптотически устойчивым. В !текоторых технических задачах недостаточно исследовать устойчивость дпижения в малом. 1огда следует отбросить ограннче1П1я, паложешп.1е на отклонения начальных условий нозмушенно10 движения, от начальных условий невоз,\!уш,енного движения. Иевозмушенпое движение системы называется асимптотически ус-тойчиВ.!м в боль!иом, если при любых иных начальных условиях, чем (3*), pemeiHie системы ура1итений (1*), начиная с 1!екоторо10 определс1Н10го значения врсме1ш, будет отклоняться от решения (2*) на величину, MenbHiyio наперед зэдшпюй. Отклоне1шя начальных условий движения от заданных ypainienn-нми (3*) называются возмун,еиия.мн. Возможны и другие оиреде.тсния устойчивости движении. В частности, ко МН01ИХ задачах coBpeMeiuiotl техшн<и важно обеспечить ма-.тые отклоне1!ия в peineimn д|1()фсренциальных уравнений возмуш,ен-ного движения от ре1ие1!ия невозмущенного движе!шя на конечном интервале времени. При рс!пенпп задач на устойчивость движения !t этом !1ункте будет нриме!!ен пря.мой метод щггегрнрочания дll(j)(jJepeнциaлыF!,!x уравнений возмущенного движения. Этот метод наиболее эф(1:е1ст1:нен но своим результатам, однако ею применение 01ра11ичено нсОольнгчм чистом во.тможных приложений ввиду математических трудностей, связанных с 1голучениел1 решения в замкнутом штдс. При р е ш е и и и з л дач на устой ч и в ость л. в н ж синя прям 1,1 м м е т о д о .\ и н г е г р и р о в а и и я д и с() () е р е н ц и а л ь -и ы X уран и е и н й п о з м у щ е н и о г о движения рекомендуется следую п1 и й и ij рядок действий: 1) состав.1яем днфференцнтльные уравнения пепозмущениого движения систем!.!; 2) паходиУ! часг!1ое ре1Н(.т!ие этой систоп.! лт!)(()ор(М1!и1а.ты!ых ура1П!е!!ий, соответст11у;о!н,ее :;ала1нн.!м !ia4a.Tb!!UN! усло!!иям и опре-де.тяющее !ie!t03MyiuC!!H0( дв1г,ке1!ис системь!; 3) задаемся другими !1ачалы!ь!МИ ycлO!iия!и Д!и1же!1ия; 4) составляем ;и1ффере1!!1иалы!ые ура!ще1!ия Bo:niyi!iCi!HOi0 д!!11-жспня; 5) ипте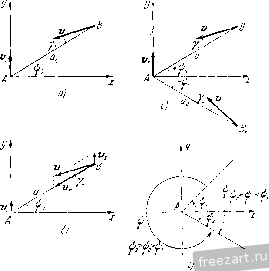 К аалачо ИИ. гoл 7, образовл1нн>1й скоростью точки Д с линией называ- ется уг.том упреждения. Точк;. /1 бу.тет сблнжатт.ся с точкой Л, вплоть до Ч0ЧН01Ч) попада1гия, но нрям()лп1е/ноП относительной траектории, если выбрать утол упреждения 7 сог.тасно paiiencTBy SHI 7,1 = - cos 60 = к cos 60, так как при этом относительная скорость точки В будет нлпрлв.1епа но ЯЛ (рис. а). Равенству (1) соответствуют два значения yi-.Ta:L6,) (рис. 6): sm <о= у --- Таким образом, прямо.тннейиое двнже1Н1е точки Я возможно ири подходе к точке Л с передней полуплоскости и с задней но.тунло-скости, по нря.\н.тм ВА и Д,Л. Определить усто11чивость движения точки В по ВЛ п BiA. 1пСл = 1п \ -k-\- SIB-,сг 1-- у к'- sm-f sin U sin 7 - k COS Jj где С-произвольная ностоя1шая, а через k обозначено отношение скоростей Л = -. Освобождаясь от логарифмов и определяя С по начальным условиям (при / = 0 а = а^, = имеем: - - /г -f sin тс(Я'у„ - - Ук- S111-7 sm sin 7 - й cos i -/г + sm 7С05 6-L y/i- - siri- siri 6 siriY -fccos sm r sill T - A: cos -bg , sill Y crjs j Это уравнение относитетыюй траектории точки В в возмущенном движении. Решение. Рлссматривая движение точки В как сложное движение, складываюн1ееся из нерсиосного движения вместе с точкой А и относительного движения но отношению к точке Л, замечаем, чю при соОлюдспип равенства (1) вектор относительной скорости точки В направлен в точку А (рис. в). Наблюдатель, движущийся вместе с точкой А, видит точку В, двгжущейся по прямолинейной относительной траектории В А с постоянной скоростью v. Эю и будет иевозмушенпое движение точки В. Рассмотри.м теперь возмуи,енное дритжение точки В, полагая, что угол упреждения [ не удовлетворяет равенству (1). Обозначая расстояние АВ через а, находим проекции относительной скорости па ЛВ и на ось, перпендикулярную < ЛВ: а = -ZJCos-; - z) sin i, (3) al = vi\n{-cos 6. (4) В этих уравнениях через iJj обозначен угол между осью х и прямой ЛВ в данный момент времени. {азделим уравнение (3) иа [)авецство (4) и нохшожим обе части на d<. Тогда найдем: d a -jcos-f-f o.sin l . a crsy -V sm 7 При интегрировании этого уравнения с разтеле11пыми переменными необходимо рассмотреть три частных случая: 1) sin-;</t2; 2) %т'-{ = к'-; 3) sin-7>A-. Первый случай: (ма.тый угол упреждения: 51П'--,<А^). Ин1ег[)ируя (5), находим: ros f / Т - ens i \ VkT:- COS 7 Если к<\, то точка В насгигнст точку А при угле <!я, определенном рапенстпами 1 sin v . , 1 / , sin-7 COS 6, = -, .sm.2 = -]/ 1--(9) так к'ак тогда а обратится и нуль, что следует из (7). Сопоставляя значе1П1я 0. (9) с рявенствами (i) и (2), заключаем, что угол (J<a = - t, для угла упреждения 7. Иначе говоря, в конце движения точка В выходит на rpaeicTopnio певозмущепного движения, находящуюся в задней полуплоскости. Следовательно, движение по относительной траектории АВ, находящейся иод углом (-к оси х, устойчиво ii большом. Каково бы ни бмло начальное во:муи|,ение, точка В в копне движения вернется на прямую А В. С другой стороны из равенства (4) имеем: ,1п,-г,.сояО (10) Следовательно, при переходе через прямую, расположенную под уг.мом i)u определяемым равенствами (рис. г) sin 7 . . т / , sin-7 Cos<!, = -, sni y 1--v , (II) угловая скорость прашепия липни AR меняет знак. Если начальный угол i!)o меньше i, и болыпе Ь^, то и процессе движения угол i моноюпно уменьшается вплоть до - .i, когда точка В совмещается с точкой Л. Если же угол бо больше 6 но меньше ti, то угол в процессе движения монотонно упеличив.чется вплоть до = <., при котором опять-таки точка В совмещается с точкой А (рнс. г). Следовательно, певозмущепное движение по относительной траектории АВ, расположенной в передней нолуп.тоскостп, неустойчиво в малом. Как бы ма.то ни бы.ю отк.тонение точки от траектории невозму-щенпого движения, находящейся в передней полуплоскости, она при дальнейшем движении будет щ'е дальше отклоняться от нено.чмущеп-ной траектории, приближаясь к другой прямолинейной траектории невозмущепното движения, рЕсноложенноИ н задней полуплоскости. Второй случай: (siir-7 = Л ). Интегрируя уравнение (о) и определяя произво.тьную постоянную ишегрирования по начальным условиям Заметим, что при разных k показатель степени различен: > I при к< 1 = 1 при к=\ (8) < ] при к^\. 650 УСТ0Й'1ИВОСТ[. РЛтЮВР.СИЯ и М\ПЫЕ ДВИЖЕНИЯ СИСТР.Л^М [ГЛ, XHI (при t = (j а - а( (!i = (jq), находим уравнение относительном траектории возмунтенного дгнгжения l\-li- / с Си , Ура1И1СНие (10) в :-лом случае нрнпимаст вид ф=-(1 - cos <;j). (13) Следовательно, угловая скорость поворота л^инии ВА всегда положительна. Из уравнения (12) следует-, что расстояние а об1)аи,ается в нуль при ij)->-0 с отрицательной стороны. Таким образом, в этом случае обе траектор)ни невозмущенпо! о движения ([)ис. г) сливавотся в одну прямую Лх, углы <!1 н оброщаются соответственно в нуль. П этом случае с.тедует судить об устойчивости двтгжения но прямой Ах на основании знака возмущения. Если начальное отклонение находится в первой четверти, то точка В будет отклоняться все дал1>шс от пря-MOfi Ах и совпадет с точкой Л ири (jj-> О с отрицательной стороны. Если начальное отклонение лежит в четвертой четверти, то точка В будет приближаться к прямой Лх, угол ij будет ст1)емнться к нулю. В этом случае движеште усгойч1ШО в большом. Третий случай; (siny )- Интегрируя уравнение (5) и определяя произвольную ностоя1шую интегрирования по начальным условиям (а = аа, - а п|)и /=0), накодим ypainicnne относительной траектории возмущенного лвиже1Н1я а / sin [ - k cos , 1/мТ7 1~Г t \ . (л / bin-; l-T . С, о \ , cos i 2 10. 7 (14) Из этого уравнения сле.тует, что расстояние до точки А обращается в нуль при пеограниченном возрастании угла Из уравнения (4) находим уг.товую скорость поворота прямой С-{sin у-А cos iji), (15) откуда следует, что yi лоиая скорость не меняет знака. Ее знак совпадает со знаком sin у. Таким образом, возмущенная-траектория точки В - cimpa.Mb, проходящая через точку .4. Из уравнения (15) следуег, что угловая скорость в[)а1цення н[)ямой ВА по мере ириближегшя точки В к А иеограничеппо воз-р;1стает. 1 ... 61 62 63 64 65 66 |
 |
 |