

 |
 |
|
Навигация
|
Главная » Мануалы Тогда что и требовалось доказать. § 21. Уравнения равновесия системы сил, произвольно расположенных на плоскости Для сил, произвольно расположенных на плоскости, имеются два условия равновесия: M = Mi =0; R* = Yx-{-r=o. (21.1) Из второго условия (21.1)следует, что X=Xi=0 и Y= Yi=0. Таким образом, два условия равновесия сил, произвольно расположенных на плоскости, можно выразить в виде системы трех уравнений: 2 5.= О, (21.2) Эти уравнения называются основными уравнениями равновесия плоской системы сил (I система уравнений). Центр моментов и направление координатных осей для этой системы уравнений можно выбирать произвольно. Существуют и две другие системы трех уравнений равновесия сил (И и III системы): 11- lii=0; ] 111. 2а1.д = 0; (21.4) При этом в системе II ось и не должна быть перпендикулярна прямой, проходящей через точки Л и fi, а в системе III точки А, В н С не должны лежать на одной прямой. Покажем, что при этих условиях системы II и III являются уравнениями равновесия плоской системы сил. Пусть дапа система сил, произвольно расположенных на плоскости, Pj, Pj.....Р„ (рис. 58), удовлетворяющая трем уравнениям (21.3): причем ось и не перпендикулярна прямой АВ. Известно, что неуравновешивающиеся силы, произвольно расположенные на плоскости, приводятся или к паре сил или к равнодействующей (см. § 20). Так как главные моменты системы сил относительно двух центров равны нулю, то рассматриваемая система сил не приводится к паре сил. При наличии пары главные моменты системы сил относительно всех точек плоскости одинаковы и равны моменту этой пары (см. теорему о моменте пары сил § 13). Если силы приводятся к равнодействующей силе, то ее линия действия должна проходить через точки А и В, так как на основании теоремы Вариньона Рис. 58. Но проекция равнодействую- щей на любую ось равна сумме проекций составляющих сил, т. е. /? cos а = 2 t/j = 0. где cosa=0, следовательно, предполагаемая равнодействующая R = Q. Таким образом, II система уравнений показывает, что данная система сил не приводится ни к паре, ни к равнодействующей, следовательно, она уравновешивается. В случае, если ось и перпендикулярна прямой АВ, то П система уравнений справедлива и при наличии равнодействующей, для которой АВ является линией действия. Пусть плоская система сил удовлетворяет трем уравнениям: 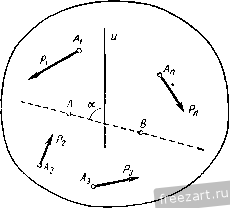
причем точки Л, В и С не лежат на одной прямой. В этом случае силы не приводятся к паре сил, так как главные моменты этих сил относительно трех центров равны нулю. Силы не приводятся и к равнодействующей силе, так как если она существует, то линия ее действия не может пройти через три точки, не лежащие на одной прямой. Следовательно, рассматриваемая система сил уравновешивается и III система уравнений является системой уравнений равновесия плоской системы сил. Итак, установлено, что число уравнений равновесия плоской системы сил равно трем. При помощи этих уравнений можно решать задачи статики на плоскости, в которых число неизвестных не превышает трех. § 22. Сложение параллельных сил на плоскости. Уравнения равновесия параллельных сил. Положим, что даны параллельные силы Pj, Pj, ..., Р„, расположенные на плоскости и приложенные в точках А^, ..., Л„. Приведем силы к произвольному центру О. Получим в этом центре силу R*, равную главному вектору, и пару сил с моментом Ж. Вычислим проекции главного вектора на координатные оси д:, у, направив ось у параллельно силам: где К,= + Р(, если направление силы Р; оси у, и V1 = - Pj. если направления силы ложны. Так как X = О, то главный вектор При K=2i(>0 направление главного вектора R* совпадает с направлением оси у, а при K = 2iP/<0 направление R* противоположно направлению оси. Таким образом, имеем: совпадает с направлением Р; и оси у противопо-R направлен по оси у. м о т. е. главный вектор системы параллельных сил параллелен силам, его модуль равен абсолютному значению алгебраической суммы проекций сил на ось, па- О, раллельную силам, а его направление определяется знаком этой суммы. Момент пары сил, эквивалентной системе пар, появившихся в результате приведения, равен главному моменту параллельных сил относительно центра приведения: Рис. 59. или 4 А. А. Яблонский Для параллельных сил на плоскости возможны все те же случаи приведения, что и для сил, произвольно расположенных на плоскости (§ 20). Параллельные силы, если они не уравновешиваются, можно привести или одной силе, или к паре сил. Для системы параллельных сил на плоскости имеем два условия равновесия: М=0 и /?* = 0. Для получения уравнений равновесия одну из осей координат; например ось у, направляют параллельно силам. Тогда все силы проектируются на ось у, а проекция каждой силы на ось х равна нулю. Два условия равновесия системы параллельных сил на плоскости можно выразить в виде двух уравнений: Эти уравнения называются основными уравнениями /?й8ковесая параллельных сил на плоскости (I система уравнений). Центр моментов для этой fi,<f I системы уравнений можно выбирать /3° произвольно. tv Существует и другая система двух Рис 60 уравнений равновесия параллельных сил-И- Sf> = 0; При этом прямая АВ не должна быть параллельна силам. II система уравнений показывает, что силы не приводятся к паре сит (рис. 60) и к равнодействующей силе, так как линия ее действия, параллельная силам, не может пройти через точки А щ. В. § 23. Статически определенные и статически неопределенные задачи. Определение реакций внешних и внутренних связей системы взаимосвязанных тел Статически определенными называют задачи, которые можно решать методами статики твердого тела, т. е. задачи, в которых число неизвестных не превышает числа уравнений равновесия сил. Статически неопределенными называют задачи с числом неизвестных, превышающим число уравнений равновесия сил, т. е. задачи, которые нельзя решать методами статики твердого тела и для решения которых нужно учитывать деформации тела, обусловленные внешними нагрузками. Для решения задач на равновесие сил, приложенных к твердому телу и лежащих в одной плоскости, можно пользоваться тремя уравнениями равновесия сил. Такая задача статически определенна, если число неизвестных не больше трех. Если к телу приложена система параллельных сил, то можно воспользоваться только двумя уравнениями равновесия сил. Эта задача статически определенна, если число неизвестных в ней не превышает двух. Для параллельных сил, приложенных к системе п тел, можно составить по два уравнения равновесия для сил, приложенных к каждому из этих тел, т. е. всего 2п уравнений равновесия. Если же на эту систему действуют силы, произвольно расположенные на плоскости, то общее число уравнений равновесия сил, приложенных к системе и тел, равно Зге. Рассмотрим некоторые статически определенные и статически неопределенные задачи, в которых по заданным силам требуется определить реакции опор. На рис. 61а изображена балка на двух опорах, находящаяся под действием двух заданных непараллельных сил Р и Q. Так как опора А неподвижна и линия действия ее реакции не известна, то реакция должна быть разложена на две составляющие по осям д: и у. Если будут найдены эти составляющие Хд и Уд, то модуль и направление реакции Рд определятся согласно § 9. Реакция опоры В как шарнирной опоры на катках направлена перпендикулярно к опорной плоскости и необходимо определить лишь ее модуль. Общее число неизвестных величин равно трем, т. е. числу уравнений равновесия сил. У уа а
Рис. 61а. У Рис. 616. Эта задача статически определенна. На рис. 616 изобра-J. жена балка с двумя непо-- движными опорами, находящаяся под действием сил Р и Q. Реакцию каждой из этих опор можно определить только по двум ее составляющим по осям л; и у. В этой задаче имеем 4 неизвестных и 3 уравнения равновесия сил. Следовательно, задача является статически неопределенной. На рис. 62 изображена двухшарнирная арочная ферма, нагруженная силами Р и Q. Пяты арки шарнирно прикреплены к неподвижным опорам Л и fi. Реакции этих опор определяются по двум составляющим по осям х и у. Задача содержит 4 неизвестных. а число уравнений, в которые входят неизвестные, равно трем, т. е. она статически неопределенна. Применяются конструкции, представляющие собой систему отдельных твердых тел, связанных между собой. Примером такой конструкции является трехшарнирная арка (рис. 63). В такой конструкции связи, соединяющие ее отдельные части, называются внутренними (на рис. 63 шарнир С), а связи, соединяющие ее с телами. 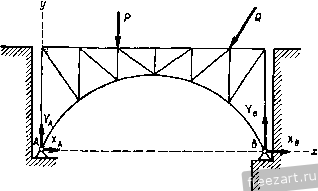 Рис. 62. в нее не входящими (опорами), называются внешними (на рис. 63 шарниры А и В). Для определения реакций связей такую конструкцию мысленно расчленяют на отдельные тела и каждое тело рассматривают как 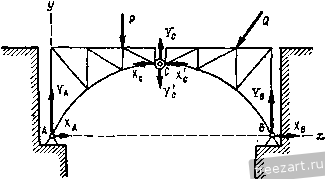 Рис. 63. свободное, находящееся под действием задаваемых сил и реакций внешних и внутренних связей. Для сил, приложенных к каждому телу, составляют уравнения равновесия. Если число неизвестных сил не превышает числа уравнений равновесия, то задача статически определенна. Так, на левую полуарку системы, изображенной на рис. 63, действуют: задаваемая сила Р, реакция внешней связи-шарнира а в виде составляющих Хд, Уд и реакция внутренней связи шарнира с в виде составляющих Х^ и У^- Соответственно на правую полуарку действуют силы Q, Х^, У^, Х^, У^, При этом реакции внутренних связей попарно равны по модулю и противоположны по направлению, т. е. х,х',. Составив по три уравнения равновесия сил, приложенных к каждой полуарке, получим шесть уравнений, содержащих шесть неизвестных величин xj, Кд, х^, Кд, х^ у^., т. е. данная задача статически определенна. Так решены примеры 12 и 15. Однако, реакции опор трехшарнирной арки (рис. 63) удобнее определять так, как это сделано в примере 16. Рассматривая арку как одно твердое тело, составляют три уравнения равновесия действующих на нее задаваемых сил Р и Q и реакций внешних связей Хд, Уд, Хд и У^. Затем, расчленив ее, составляют три уравнения равновесия сил, приложенных к одной части, например, левой - Р, Хд, Уд, Х^, Ус- В этом случае система уравнений решается проще и реакции внутренних связей определяются в последнюю очередь. § 24. Примеры на равновесие параллельных сил на плоскости Пример Ю. Однородная горизонтальная балка ав, весом g~2 кн, опирается на стену в точках в и d. Вес подвешенного груза р = 1 кн. Размеры: ав = 4м, db -0,5 м. Определить реакции опор d и в (рис. 64а). Решение. Руководствуемся изложенным выше планом решения ,задач статики, рассматривая равновесие сил, приложенных к балке ав. а с Рис. 64а. Рис. 646 1. Показываем действующие на балку заданные силы: вес груза Р в точке а и вес балки G в середине балки с (рис. 646). 2. Освобождаем балку от связей, заменяя их действие реакциями опор Rb и Rjj, направленными перпендикулярно к поверхности балки. в этой точке 3. К полученной системе вертикальных сил Р, О, R, R, действующих на балку АВ, применяем условия равновесия сил в виде двух уравнений равновесия параллельных сил на плоскости: Sp.o. j При составлении алгебраической суммы моментов сил относительно точки пользуемся правилом знаков, изложенным в § 12. При этом сумму моментов сил составляем относительно точки, в которой приложена одна из неизвестных сил. В этом случае сила, приложенная не имеет момента относительно нее и уравнение содержит только одну неизвестную величину. Составляем сумму моментов сил относительно точки В: 2m, = 0, P-BA-JrQ-BC-RoBD = 0. При составлении алгебраической суммы вертикальных сил условимся силы, направленные вверх, брать со знаком плюс, а направленные вниз - со знаком минус; 2я, = о. -Р 0+/?в -/?5 = 0. 4. Из первого уравнения определяем модуль реакции опоры R: находим из Рис. 64в. Определив R, опоры R: /?==-p-g + /?, = -10-2 + -j-88 = 76 кн- P-BA+G-BC 10-4-f 2-2 88 кн. BD 0,5 второго уравнения модуль реакции Рис. 64г. Проведем анализ полученных результатов. Значение обеих реакций получено со знаком плюс потому, что на расчетной схеме (рис. 646) указано действительное направление этих реакций: вверх для реакции Rq и вниз для реакции Рд. Воздействие двух опор D и В на балку можно представить в следующем виде. Разбиваем реакцию R, на две силы Rd и Rd такого же направления, имеющие модули (рис. 64в): /?о = Рд=76 кн; r o = Ro - Rs=12 кн. Силы Rd и Rb составляют пару сил с моментом I ЖI = DB = 76 0,5 = 38 K л. Кроме пары сил, имеется вертикальная реакция Ro(/?o=12 кк), приложенная в точке D и направленная вверх (рис. 64г). Пример 11. Горизонтальная балка АВ, длиной =1,2 м, поддерживающая балкон, заделана в стену. На балку действует равномерно распределенная нагрузка интенсивностью =1,25 к/л. Определить реакции заделки (рис. 65а). Решение. Рассматриваем равновесие сил, приложенных к балке АВ. Равномерно распределенную нагрузку можно заменить сосредоточенной силой Q - равнодействующей системы равных парал-
Рис. 65а. Рис. 65ff. дельных сил, приложенной в середине загруженного участка АВ. Модуль этой силы определяется: Q = /= 1,25 KHJM 1,2 M=l,5 кн. Реакции заделки представляют собой силы, распределенные по всей опорной площади, причем на нижнюю поверхность балки действуют силы, направленные вверх, а на верхнюю-силы, направленные вниз. Из этой системы сил образуется вертикальная реакция опоры (если все заданные силы вертикальны) и реактивная пара сил, препятствующая вращению балки вокруг закрепленного конца (см. пример 10). Момент этой пары сил называется опорным моментом. Показываем на схеме (рис. 656) реакцию заделки и реактивную пару с моментом М. Условимся направлять реакцию опоры вверх, а реактивную пару против движения часовой стрелки. Истинное их направление определим по знаку ответа. Составляем два уравнения равновесия параллельных сил на плоскости. При этом сумму моментов всех сил составляем относительно точки В, так как в этой точке приложена неизвестная реакция опоры R. Сумму моментов сил реактивной пары относительно точки В включаем в уравнение в виде момента пары М, согласно § 13. I. 2].й = 0, Q + Ж^О; M = ~Q-=-1,5 0,6 = -0.9 кн - м. Момент получен со знаком минус, следовательно, реактивная пара сил имеет направление, противоположное принятому на рас- четной схеме, т. е. пара направлена в сторону движения часовой стрелки. П. 2Л=0; -Q + /?3 = 0; P5 = Q= 1,5 кн. Знак плюс показывает, что реакция направлена так, как принято на расчетной схеме, т. е. вверх. Пример 12. Балка моста состоит из двух частей AD и DC, соединенных между собой шарниром D. Собственный вес погонного метра моста , = 10 khjm, вес погонного метра поезда 2 = 20 khjm. Определить реакции опор балки при условии, что поезд находится на участке АЕ (рис. 66а). 20м гпм Рис. бба. Решение. Рассматриваем равновесие сил, приложенных к балке АС: равномерно распределенной нагрузки от собственного веса балки, веса поезда и реакций опор Рд, Рд и R,. Так как реакции опор Л и В и равномерно распределенная нагрузка вертикальны, то уравновешивающая их реакция неподвижной шарнирной опоры С должна быть тоже вертикальна. 20 м А В
Rc с Рис. 666. Рис. 66в. Таким образом, имеются три неизвестные вертикальные реакции опор, R, Rb и Rc- Определить их модули из двух уравнений равновесия параллельных сил, приложенных к балке АС, невозможно. Так как балка АС представляет собой систему двух тел, соединенных шарниром D, то расчленяем ее на части AD и DC и рассматриваем равновесие сил, приложенных к каждой части (рис. 66 б,в). 1 2 3 4 5 6 7 8 ... 44 |
||||||||||||||||||||||||||||||||||||||||||
 |
 |