

 |
 |
|
Навигация
|
Главная » Мануалы Ускорение точки А находится по формуле где осестремительное ускорение равно по модулю и направлено по кратчайшему расстоянию от точки А к мгновенной оси, т. е. по /г, (рис. б); первая составляющая вращательного ускорения равна и направлена параллельно оси х (в положительную сторону); вторая составляюпгая вращательного ускорения равна по модулю и; р = !е.ХГд| = £2Г = 4гй/* и направлена от Л к Б. Заметим, что ускорение точки, движуигейся по окружности радиуса h (рис. б), может быть найдено по формуле где нормальное ускорение равно р й и направлено от А по кратчайшему расстоянию к оси z. Касательное ускорение равно w\ = !1a=V2 rk dt и направлено параллельно оси х. Сопоставляя оба решения, замечаем, что )р - = щуР cos 45° и проекция ускорения течки А иа ось z равна пулю: - cos 45° - - 0. Ускорение точки А расположено в плоскости, параллельной ху. Для приобретения навыков в решении задач на вращение твердого тела вокруг неподвижной точки рекомендуется решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, издания 1950 г. и более поздних лет: 596, 698, 599, 604, 607, 610. § 2. Сложение вращений вокруг пересекающихся осей Если твердое тело одновременно участвует в двух враще1щях вокруг пересекающихся осей, то одно нз этих движе1и1й принимается за перенос1юе вращение, а второе - за от1Юсительное. Обозначая мгновенные угловые скоросги переносного движения через и от- 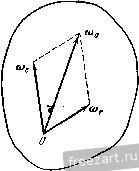 найти мгновенную угловую скорость абсо-люпюго движения (о^ по формуле (рис. 7.4) (1*) ш„ = (й. Таким образом, результирующее движение также является вращением твердого тела вокруг неподвижной точки. Поэтому все сказанное в предыдущем параграфе от1Юсительно определения скоростей и ускорений течек твердого тела, нахожде1Н1я уравне1Шй подвижного и неподвижного аксоидов, углового ускорения может быть применяю в дан1Юм случае. Наряду с этим при решении задач в этом параграфе может быть использован и другой способ. Определение скоростей точек твердого тела может быть произведено иа основании теоремы сложишя скоростей Рис. 7.4. (2*) где Va - абсолютная скорость точки; v,. и v - соответстве1НЮ ее переносная и огносительная скорости. Для онределе!щя ускорений точек можег быть применена теорема сложения ускорений (теорема Кориолиса) Wa = w,--Wr-\--w (3*) где - абсолютное ускорение точки; Wf w, - соответственно переносное, относителыюе и кориолисово ускорения. Кор1юлисово ускорение определяется формулой При решении задач на сложение вращений вокруг пересекающихся осей могут быть использованы два способа. Первый способ. По задаш1ым угловым скоростям переносного и относителыюго врапьений определяется абсолютная угловая скорость и, лалее, соглас1Ю последовательности действий, усгановлен-ноИ в § 1 этой главы, находятся все искомые величины. Второй способ. Рекомендуется такая последовательность действий: 1) выбираются неподвижная система координат так, чтобы ее ось Z совпала с переносной угловой скоростью о), и подвижная система координат так, чтобы се ось совпала с относительной угловой скоростью (О/, 2) по известным переносной и относительной угловым скоростям находится абсолютная угловая скорость; 3) определяются искомые скорости точек в относительном и переносном вращениях и, далее, искомые абсолютные скорости; 4) находятся переносное, относительное и кориолисово ускорения и, далее, искомое абсолютное ускорение точек твердого тела путем векторного сложения или сложением при помощи метода проекций. Задача 7.4. Шарикоподшипник (рис. а) состоит из неподвижной обоймы N, внутре1шей обоймы М, вращающейся покруг всртикальгюй оси Z с угловой скоростью 0), и шарика О, зажатого между обоймами. Определить положение оси z, при котором шарик будет катиться по обоймам Ж и без скольжения. Пользуясь чертежом к дагшой 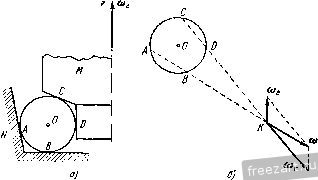 К задаче 7.4. задаче, найти графически абсолютную угловую скорость шарика и его относительную угловую скорость но отношению к вращающейся обойме УИ, если о) задана. Решение. Будем исходить из условия, что шарик О катится по обоймам М. \\ N без скольжения. Следовательно, точки Л, В шарика, находящиеся в соприкосновении с неподвижиой обоймой N, имеют скорости, равные пулю. Абсолютная мгновенная ось шарика должна проходить через эти две точки. Проводим (рис. б) прямую ш через эти две точки. Точки шарика С, Д находящиеся в соприкосновении с вращающейся обоймой М, должны иметь одинаковые абсолютные 16 М. и. Бать и др., т. I 180-6 скорости с точками обоймы М. Значит, относительные скорости течек шарика, соприкасающихся с точками обоймы М., равны пулю. Следовательно, относительная мгновенная ось шарика проходит через точки соприкосновения с вращающейся обоймой М.. Проводим (рис. б) эту прямую (О,. Находим точку пересечения К прямых (о и (о,. Движение шарика без скольжения будет дости1нуто, если вертикальная ось z будет проходить через точку К- Точка К будет оставаться неподвижной во все время движения. Задача 7.5. В механизме маятниковой мельницы (рис. а) главный вал / соединен с ведущим валом посредством шарнира Г'ука. На К01ще главного вала жестко закреплен бегун /. При достаточно большом числе оборотов ведущего вала бегун прижимается изнутри к стенке цилиндрической чаши так, что сечение бегуна Ж,Л1 катится по чаше без скольжения. Радиус этого сечения виден из центра шарнира под углом а. Угол между главным валом и ведущим валом 8. Найти угловую скорость вращения бегуна вокруг его оси симмет-рии, если известна угловая скорость ведущего вала. Решение. Движение бегуна рассматриваем как сложное, состоящее из вращения вокруг вертикальной оси и вращения вокруг оси симметрии. Вращение бегуна вокруг вертикальгюй оси (вала ) прини.маем за переносное, вращение вокруг оси симметрии (вала /) назовем относительным. Мгновенная ось абсолютного враптения - это линия, соединяющая две неподвижные течки О и УИ. Вдоль линии ОМ направлен вектор абсолютной мгновенной угловой скорости Юд. Вектор переносной угловой скорости (0 направлен по оси ведущего вала. Вектор относительной угловой скорости (О,- (это искомая в задаче скорость вращения вокруг оси симметрии) направлен по главному валу /. Предположим, что для наблюдателя, смотрящего на мельницу сверху, бегун движется по часовой стрелке. Тогда вектор переносной угловой скорости (0 направлен вертикально вниз; основное векторное соотношение 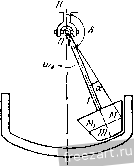 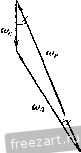 к задаче 7.5. §21 СЛОЖР.НИЙ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ представлено на рис. б. Рассматривая треугольник, образованный векторами (Од, (Og и (0, имеем по теореме синусов sina sin[180° -а -(180° -8)] или sin а sin (8 - а) откуда окончательно находим: sin (8 - а) sm 1 Задача 7.6. Искусственный спутник Земли, двигаясь по круговой орбите, имеет период обращения, вычисленный по отношению к системе 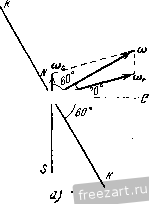 W-------- fi- 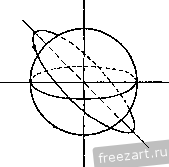 К задаче 7.6. координат, движущейся вместе с центром Земли поступательно, равный 1,5 часа. Определить его относительную угловую скорость по отношению к Земле, вращающейся вокруг своей оси, при угле наклона его орбиты к экватору а, = 60°. Вектор его угловой скорости <о образует острый угол с осью 5Л^ Земли. Р е ш е н и е. Плоскость орбиты К,К образует с экватором W0 угол 60°. Тогда вектор абсолютной угловой скорости спутника (о составляет угол 60° с осью SN, по которой направлен вектор угловой скорости Земли. Рассматривая вращение спутника как движение, складывающееся из переносного вращения вместе с Землей и искомого относительного вращения по отношению к Земле, имеем: м -L. 0), где (О - абсолютная угловая скорость спутника; - его относительная угловая скорость. Величина абсолютной угловой скорости 2п Ш = мин Величина переносной угловэй скорости 2ж ~~ 24 60 мин Таким образом, в треугольнике угловых скоростей известны две стороны (1) и (1) и угол между ними. Определяем третью сторону треугольника: = V - + - 2w<u, cos G0° = g у I -i- 0,0675 мин Находим угол, образованнь[й ia с экватором: cos ( ;>O) = :i£2i° = 0,89. - это угловая скорость спутника относительно Земли. Задача 7.7. Конус А с углом при вершине, равным DOC= 90°, имеет неподвижную точку О и катится без скольжения по неподвижному конусу В, угол которого при вершине также равен 90°. Диаметр 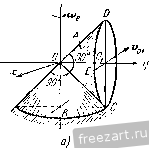 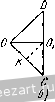  1 \ 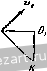 К задаче 7.7. основания подвижного конуса DC= 40 см. Скорость точки Oi по величине постоянна и равна z/o, = 80 см/сек. Найти (й^ - переносную угловую скорость конуса (вокруг оси z), его относительную угловую скорость ш,. (вокруг оси симметрии 00,) и абсолютную угловую скорость <o. Определить скорости точек D, Е, С конуса (рис. а). Решение. Точка 0\ лежит на относительной мгновенной осн вращения 00] и, следовательно, ее относительная скорость -о^ равна пулю. Согласно теореме сложения скоростей и, следовательно. 80 г с-с- -1 Учитывая направление скорости точки 0\, проводим от С к О (рис. в). Направление относительной мгновенной угловой скорости совпадает с прямой 00\. Строим (рис. в) на векторе <o, как па диагонали, параллелограмм угловых скоростей откуда следует, что величина <л. = ш^ = 4 сек'К Переходим к определению скоростей точек D, Е, С конуса. Скорость точки С равна нулю, так как эга точка лежит на мгновенной оси абсолютного движения и соприкасается с боковой поверхностью неподвижного конуса В. Найдем величину скорости точки D. Величина скорости точки D равна произведению величины абсолютной угловой скорости на при учете равенства tiQ = 0 имеем: Величина переносной скорости равна произведению радиуса вращения вокруг переносной мгновенной оси z на модуль переносной мгновенной угловой скорости: vf, =00 ш , Oi 1 е ~ 00, ~ Об, ~ 20 ~ Полагая движение точки Oj происходящим против часовой стрелки, если смотреть с ноложительно10 направления оси 2, вектор следует направить по оси г вверх. Скорости точек подвижного конуса, находящихся в соприкосновении с поверхностью неподвижного конуса, равны нулю, так как конус А катится без скольжения по конусу В. Следовательно, образующая ОС является мгновенной осью абсолютного движения и величина абсолютной скорости точки Oj равна t<g = o,/c-! .,!, где (0 - абсолютная мгновенная угловая скорость; Oj/C - перпендикуляр, опунгеиный из точки О, на мгновенную ось ОС (рис. о). Тогда OiK=OOi sin 45° = 20i=: 14,1 см кратчайшее расстояние точки D до мгновинюй оси абсолютного движения ОС Vjy = OD- == 201/2 = 160 см/сек; 1д направлена перпендикулярно к плоскости ODC (рис. б) за рисунок. Скорость точки D .можно найти и другим способом. Действительно, скорость точки D равна сумме переносной и относительной скоростей переносная скорость по величине равна z,=00j u) = 20.4 = 80 см/сек и направлена перпендикулярно к плоскости ODC за рисунок; модуль относительной скорости течки D v=Op ш^=20-4 = 80 см/сек. Так как относительная скорость совпадает по направлению с переносной скоростью, то 0 = 0-- ti = 160 см/сек. Переходим к определению скорости точки Е. На рис. г представлена плоскость OjEK, перпендикулярная к абсолютной мгновенной оси ОС и проходящая через диаметр основания конуса ОуЕ. Из рис. г видно, что кратчайшее расстояние от точки Е до прямой ОС равно ЕК = V(OiKT + {EOif - 1/200 400 = 24,5 с.и, следовательно, величина скорости точки Е будет: VpEK- --= 24,5 .5,66 = 138,5 см/сек. Эта скорость (рис. г) лежит в плоскости О^ЕК н направлена перпендикулярно к прямей ЕК- Задача 7.8. В условиях предыдущей задачи определить абсолютное и относительное угловые ускорения конуса А. Найти ускорения точек Oi, D, С. Решение. Угловое ycKopetme может быть определено как скорость конца вектора угловой скорости. Угловая скорость переносного движения (0 сохраняет без изменения свою величину {(л^ = 4 се.к~) н свое нанравление (по оси z). Угловое ускорение в абсолютном движении равно 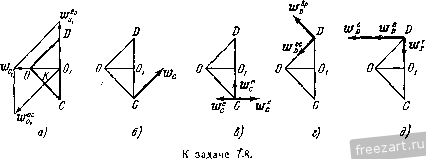 Для определения углового ускорения можно воспользоваться теоремой сложения угловых скоростей: а = + г. где (Оц, (0, <а^ - соответственно абсолютная, переносная и относительная угловые скорости тела. Вычисляя от обеих частей этого равенства производную по времени, находим: 5 + - rfF + + -Так как в данной задаче = 0 и =гО, то Этот же результат получается и из (1), если вычислить непосредственно выражение а = X а = X {<е -f 7-) = X г' е„ = 16 сек-\ Переходим к определению ускорений точек Oj, D, С. Ускоре1ще точки Oj может б[.1ть определено тремя способами. Перв?.1й способ - точка Oj описывает окружность радиуса 00 с постоянной повеличине скоростью xiq, =80 см/сек; следовательно. (так как вектор <o вращается со скоростью (оД или Оно направлено по оси х в положительную сторону, перпендикулярно к плоскости 00]С. 488 вращение твердого тела вокруг неподвижной точки [гл. vu ускорение точки О, будет нормальным ускорением с модулем Ох=,\; = % = 20 см1сек\ оно направлено от О, к точке О. Второй способ - ускорение течки Oj, как принадлежащей твердому телу, вран1ающемуся вокруг неподвижного центра О: 0, = Ч\ -г = а X X Г) + е„ X Г, причем величина осестремигельного ускорения w = hl - О^К = У 2 10-32 = 320 j/I см/сек'. Это ускорение направлено по перпендикуляру к мгновенной оси, т. е. от О) к К (рис. а); модуль вращательного ускорения дар = ihi = £ - 00, = 16 20 = 320 см/сек\ оно направлено перпендикулярно к и г-00 т. е. но оси z вверх; замечая, что угол л:ежду гиР и равен 135°, заключаем, что =-- twP = 320 см/сск' и направлено но 00 что совпадает с результатом, найдешилм первым способом. Третий способ - ускорение точки О] определяем по теореме сложения ускорений (теореме Кориолиса), рассматривая ее абсолютное движение как составное из переносного вращения (вокруг оси z) и относительного вращения (вокруг оси OOi); тогда переносное ускорение направлено от Оу к О и равно по величине да = OOi = 20 - 16 = 320 см/сек -; относительное ускорение точки О, равно нулю, так как точка 0\ лежит на оси 00], вокруг которой происходит относительное движение конуса; кориолисово ускорение точки Оу равно Ь, = X Ь,; оно обращается в нуль, так как нулю равна относительная скорость lij. точки оу\ таким образом, как и при ранее использованных способах, величина ускорения О, будет: is)q =- ги = 320 см/сск-; это ускорение направлено от Оу к О. 1 ... 45 46 47 48 49 50 51 |
 |
 |