Промышленное охлаждение - freezart.ru. Схемы и периодика

Главная » Мануалы

1 2 3 4 5 ... 51

находится в равновесии при наличии двух связей: наклонной плоскости и выступа. Применив закон освобождаемостн, заменим действие на шар мысленно отброшенных связей соответствующими реакциями. Реакция Rj гладкой наклонной плоскости направлена к ней перпендикулярно. В точке В проведем касательную (рис. б) и направим опорную реакцию нернендикулярно к касательной. Следовательно, линия действия Rg проходит через центр тяжести шара С.

Теперь можно рассмотреть шар как свободное твердое тело, находящееся в равновесии под действием плоской системы трех сил: Р, Rj и ig, ЛИНИИ действия которых пересекаются в точке С. Для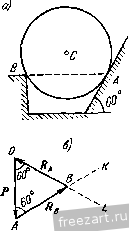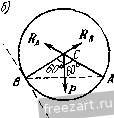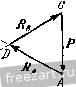

К задаче 1.2.

равновесия шара необходимо и достаточно, чтобы сумма этих трех сил равнялась нулю. Поэтому силы образуют за.мкпугый силовой треугольник.

Построение силового треуголыпша начнем с силы Р, нзвес1ной как но величине, так и но напраплегшю. Из произнольной точки О (рис. в) проведем вектор, который равен силе Р. К ксниу силы Р надо приложить начало силы R или Rj. Выбираем в качестве следующей стороны силового треугольника реакцию выступа R. Так как направление силы известно, то проведем через точку А прямую АК, параллельную линии действия реакции Rj. Для последующего построения силового треугольника надо к концу /?д приложить начало силы Лд. Сделать это невозможно, так как модуль силы R неизвестен. Несмотря на возникшее затруднение, построение силового треугольника можно успешно завершить. Следует учесть, что при равновесии шара силовой треугольник должен быть за.мкнуг. При

этом конец вектора реакции должен совместиться с началом вектора силы Р, т. е. попасть в точку О. Поэтому проведем через точку О прямую 0L, параллельную линии действия силы Лд. Точка В пересечения прямых АК и 0L определяет положение третьей вершины В силового треугольника ОАВ. В построенном силовом треугольнике должно иметь место единое направление стрелок, т. е. в каждой из вершин треугольника должен быть расположен конец только одной из трех сил.

Для определения модулей опорных реакций и Rg остается решить силовой треугольник ОАВ. Нетрудно видеть из рис. в, что углы, образованные линией действия силы Р с линиями действия реакций Rj и д, равны 60; таким образом, силовой треугольник оказывается равносторонним и, следовательно, /?д = /?д = Р= 20 л;Г.

Если бы при построении силового треугольника мы к концу силы Р приложили начало силы (а не R, как это было сделано выше), то получили бы силовой треугольник GAD (рис. г), равный силовому треугольнику ОАВ. Решение этого силового греуголышка, естественно, привело бы к тем же результатам.

Задача 1.3. Через гвоздь, вбитый в стену, переброшен трос (рис. а). Один конец троса прикреплен к полу под углом 30° к горизонту. К другому концу троса подвешен груз, вес которого Я = 100 кГ.

Определить величину реакции стены, в коюрую вбит гвоздь. Весом гвоздя пренебречь. Трос расположен в вертикал! ной плоскости.

Решение. Предварительно рассмотрим равновесие груза (рис. б). К грузу приложены: вес Р, направленный по вертикали вниз, и реакция троса Т, направленная по вертикали вверх. Воспользовавшись вторым законом о равновесии твердого тела под действием двух сил, получим:

Т=Р= 100 кГ.

Переходим к рассмотрению равновесия гвоздя. Мыс-лешю рассекая левую и правую ветви троса вблизи гвоздя, заменим действие отброшенных частей троса его реакциями Т] и Ti (рис. в). Силы Ti и Т.2 равны по модулю силе Т, но различны по направлению: \ Ti\ = \ T,i\ = \T\. Связью, наложенной на гвоздь, является стена.

Гвоздь находится в равновесии под действием активных сил н Ti и реакции R стены, направление которой неизвестно. Так как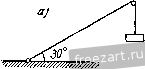

к задаче 1.3.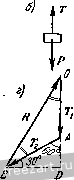

ЛИНИИ действия этих трех сил пересекаются в одной точке, то можно построить силовой треугольник иа силах Ti, и R. В данном силовом треугольнике две силы (Т^ и Tq) известны как по величине, так и но направлению. Проведя из произвольной точки О силу, векторио равную силе Тц приложим к ее концу силу, векторно равную силе Г, (рис. г).

Так как при равновесии гвоздя силовой треугольник должен бы 1ь замкнут, то, соединив начало О силы с концом В силы Тя, определим реакцию стены Л. Конец силы должен находиться в исходной точке О. При этом силовой треугольник ОАВ оказывается замкнутым.

Для решения силового треугольника ОАВ воспользуемся вспомогательными построениями. Проведем из точки В направо горизонталь и продолжим ОА по вертикали вниз до пересечения с горизонталью в точке D. В треугольнике ABD угол ABD равен углу наклона левой ветви троса к горизонту, т. е. 30°. Следовательно, угол BAD равен 60. Угол BAD является внешним по отношению к силовому треугольнику ОАВ. Замечая, что силовой треугольник ОАВ является равнобедренным (силы и по модулю равны), имеем: / ОВ.А -

= L ВОА = \ / £}ЛО = 30°. Теперь из треугольника ОАВ без труда

находим искомый модуль реакций R стены:

R = BO = BA cos 30° АО cos 30° = 2 Г cos 30° =

= 2. 100 173 кГ.

Задача 1.4. Два абсолютно жестких стержня Л5 и ЛС соединены шарниром в точке А и прикреплены и полу шарнирами В н С, образуя с полом соответственно углы 45° и 60° (рис. а). К валику шарнира А подвешен на нерастяжимой нити груз D, вес которого Р = 100 кГ.

Определить усилия, возникающие в стержнях АВ и АС. Весом стержней пренебречь.

Решение. Для определения усилий в стержнях АВ н АС следует рассмотреть равновесие шарнира А. Однако непосредственно ирисгугмггь к исследованию равновесия узла А невозможно, так как он находится в равновесии под действием трех неизвестных сил: реакций стержней АВ и АС и реакции нити AD. Поэтому для определения реакции нити предварительно рассмотрим равновесие груза D. Груз D находится в равновесии под действием двух сил: веса Р и реакции нити Т. Эти силы направлены в противоположные стороны (рис. б). Учитывая условие равновесия груза, получим, что Т=Р = = Ш к Г.

Теперь, когда одна из трех сил, приложенных к шарниру А, известна, можно изучить равновесие шарнира А. К нему приложена одна известная сила - реакция нити Т', направленная по вертикали

ВНИЗ (на основании закона равенства действия и противодействия Т'~~Т). Реакции Tg и Т^- стержней АВ и АС направлены вдоль стержней (см. на стр. 14 и iS пример 7 направления реакции связей). На рис. в эти три силы изображены приложенными в шарнире А (в общем случае трудно заранее указать, направлены ли силы Гд и

Tq вдоль стержней вверх или вниз; это будет уточнено в ходе последующего решения задачи).

При равновесии шарнира А рав1юдействующаи этих сил должна быть равна нулю, следовательно, силы Т, Tg и Т(- образуют замкнутый силовой треугольник.

Построение силового треугольника (рис. г) начнем с силы Т', известной по неличине и по направлению. Взяв произвольную точку О, приложим к ней силу 7 . Затем, проведя через начало и конец силы Г прямые 0L и SK, соответственно параллельные стержням АС и АВ, получим в нересеченин третью вершину Q силового треуголышка OSQ. Изобразив на сторонах треугольника SQ и Q0 стрелки так, чтобы сумма трех сил Г', Т, и Т^- равнялась нулю (в каждой из вершин силового треугольника OSQ должен быть расположен конец только одной из трех сил), получим направления реакций и Т(,.

Перейдя к решению силового треугольника, заметим, что / SOQ = = £ DAC=30° и Z OSQ== /. BAD = 4o°, как углы с соответственно параллельными сторонами. Следовательно, SQO= 105°. Применив теорему синусов, получим;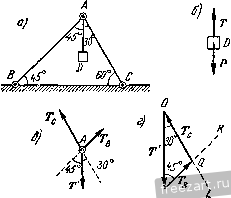

К задаче 1.4.

sin 30°

!с .

siu 45°

sin 105°

.J., sin ;ю°

sin 45° sin 105°

Подставив численные значения, находим:

7- = 51,8 1С Г, Тс = 73,2 кГ.

Задача 1.6. На рис. а изображен механизм антипараллелограмма ABCD, состоящий из абсолютно жестких стержней АВ, ВС и CD, шарнирно соединенных между собой в точках В и С и прикреплегь

пых шарнирами А и D к неподвижному звену AD; AD = BC, AB - CD. К валику шарнира С приложена направленная но горизонтали налево сила Fq=\0 кГ. (Впредь для краткости валик шарнира мы будем называть шарниром.)

Определить величину силы F, приложенной в шарнире В и направленной по вертикали вниз, если механизм находится в равновесии в положении, указанном h,i рис. а, т. е. при /iBAD = 30° и Z.OC = 90°. Весом стержней пренебречь.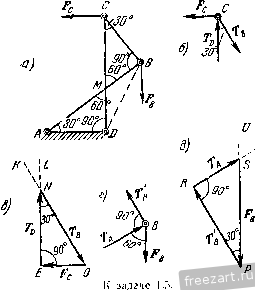

Решение. Для определения величины силы F следует рассмс т-реть равновесие шарнира В. О.анако непосредственно это сдела1Ь невозможно, так как ни одна нз трех сил, приложенных к шарниру В (сила Fi и реакции стержней ЛВ и ВС), неизвестна но величине. Поэтому для определения ветичгшы реакции стержня ВС предвари-тельрю рассмотрим равновесие ш-арЕшра С. К шарниру С нрнложена активная сила F( и реакции стержней CD и СВ. Так как стержни соединены шарнирами, то реакции направлены вдоль соотве1Ствую-nuix стержней.

Иа рисе изображен силовой треугольник для узла С Из произвольной точки О проведена сила F.. Через начало и конец силы Fc проведены прямые ОК и 1:4 соответственно параллельные стержням СВ и CD. В точке пересечения этих прямых найдем третью вершину N силового треугольника ОВМ. Направим векторы Гд и T так, чтобы сумма сил F, и 7 оказалась равной нулю.

Для определения углов в треугольнике OBN вернемся к рис. а. Соединив точки Б и D, рассмотрим треугольники ADD и DCB. Эти треугольники равны но трем сторонам, так как по условию AD = BC, AH = CD, а сторона BD у лих обшая. Воснользоиавшись равенством треугольников, найдем, что / DCB=/ DAB=30°. Теперь легко доказать расепстио треугольников AMD и СМВ. Действительно, AD = BC, / DAM = L МСВ = Ж, /. AMD= СМВ=:60°. Следовательно, Z. СВМ = L лом = 90°.

Обратившись теперь к силовому треугольнику OBN, нетрудно заметить, что Z ENO= l MC7i = 30°. Так как Pel- Т^, то получим:

Теперь мы можем определить искомую силу Fjp рассмотрев равновесие шарнира В (рис. г). К шарниру В приложены активная сила н реакции стержней АВ и ВС, направленные вдоль стержней. При эюм реакция Т' стер-жня нам извести^. Она равна по модулю силе Tf, определенной из силового треугольника OEN, и противоположно ей направлена, т. е. Tj - -(см. на стр. 14 и 15 пример 7 направления реакций связей).

Начнем построение силового треугольника для узла В с рсак-Ш и Гд, отложив ее от произвольной точки Р (рис. д). Затем, проведя через начало и конец прямые pu и rv, соответственно параллельные линиям действия искомой силы и стержню АВ, получим в их точке пересечения третью вершину 5 силового треугольника prs. Направим векторы Гд и F так, чтобы силовой треугольник prs оказался замкнутым. Так как линии действия сил Т'ц н Гд соответственно параллельны стержням СВ и АВ, то prs = = Z. Л1йС= 90°. Заметив, что rps=BAD=30°, как углы с взаимно перпендикулярными сторонами, найдем из силового треугольника prs:

Подставив значение из формулы (1), получим:

Гв = У'з с = 23,1 кГ.

Рекомендуем решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, издания 19Г)0 г. н последующих лет: 20, 24, 28, 31.

2°. Теорема о трех непараллельных силах. Если твердое тело находится в равновесии под действием трех пеиараллель-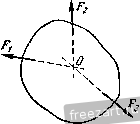

Рис. 1.18.

пых сил, лежащих п одной плоскости, то линии действия этих сил пересекаются в одной точке (pix. 1.18).

Следует иметь в виду, что пересечение линий действия трех непараллельных сил в одной точке является лишь необходимым условием для равновесия твердого тела. Пересечение линий действия трех сил в одной точке не является достаточным условием, так как равнодействующая этих сил может оказаться не равной нулю. Следовательно, достаточным условием является наличие замкнутого силового треугольника при одновременном пересечении линий действия трех сил в одной точке.

Теорема о трех непараллельных силах значительно облегчает решение задач иа равновесие твердого тела в тех случаях, когда

наиравлеиис одной из трех ураптовендинающихся сил неизвестно. Действительно, определив точку пересечения линий действия двух сил, направления которых известны, можно указать направление линии действия третьей силы, так как она должна пройти через точку приложения этой силы и точку пересечения линий действия первых двух сил.

Задача 1.6. На рис. а изображена схема супиорта универсального металлорежущего станка с закрепленным в нем резцом. К резцу в точке D со стороны обтачиваемого изделия (На рисунке изделие не показано) приложено давление N, образующее угол 30° с вертикалью и равное по модулю 300 кГ. Схематизируя опоры суппорта, считаем, что опорой А является цилиндрический шарнир, а в точке В суппорт поддерживается пружиной.

Пренебрегая весом суппорта, определить реакцию опоры и силу упругости пружины. Размеры указаны на рисунке.

Решение. Рассмотрим равновесие суппорта, к которому приложены силы: -давление обтачиваемого изделия на резсп, F - сила упругости пружины, направленная но вертикали вверх. Применив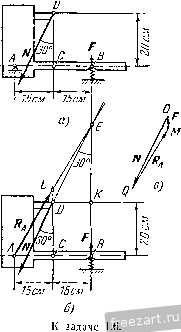

закон освобождаемости о г связей, мысленно отбросим цилиндрический шарнир А и компенсируем его действие на суппорт соответствующей реакцией Rj. Обычно мы не можем заранее указать направление этой реакции (см. пример 4 направления реакций на cip. Ii и 14). Однако в данном случае суппорт находится в равновесии под лтействием трех непараллельных сил: N, F к Поэтому можно воспользоваться теоремой о трех непараллельных силах, согласно которой линии действия сил N, F и Rj должны пересекаться в одной точке. Гак как линии действия сил N н F пересекаются в точке 10 ЛИ1И1Я действия силы R также должна проходить через эту точку (см. рис. б).

Построение силового треугольника (см. рис. в) начнем с силы N, приложив ее в произвольной точке О, взятой вне основного рисунка. Через начало О и kofich Q вектора проведем прямые, параллельные линиям действия сил F и R. В точке пересечения этих прямых найдем третью вершину М силового треугольника OMQ- Направим векторы R i\ F так, чтобы силовой треугольник оказался замкнутым, т. е. чтобы в каждой из его вершин был расположен конец только одной силы.

Для ренюння силового треугольника выполним на рис. б вспомогательное построение: проведем через точку D вертикаль до нере-сечения в точке /. с прямой ЛЕ. Нетрудно видеть, что треугольники OMQ (рис. в) и DLE (рис. б) подобны, ибо имеют соответственно параллельные стороны. Определим длины сторон треуголыпно DLE. И:! прямоугольного треугольника DKB, в котором, по условию,

DK--CIi-\o см, имеем DC=J~=2Q см, КЕDK=

Sin o(J

= \?>V:\ см. Поэтому Ш: =/Ж-l-/(20-1-1513) см, т.е.

Д£ = 46 см. (1)

Средняя линия CZ, треугольника ВАЕ равна CZ. =,j= 23 см.

Значит, DL = CL - СО = Ъ см. Для определения /.£ нредиарительно вычислим АЕ из прямоугольного треугольника АЕВ. Имеем АЕ - = У'7\В^ -г- = Т-ЗО-f 46 = 55 см. Так как AEAL-}-LE = = 21J:, то 27,5 см. Итак, стороны треугольника DLE равны

Л/: = 30 см, DL=:\ см, /.£ = 27,5 см. (2)

Мсиользовап подобие треугольников OMQ и DLE, запинюм:

F Л/

Подставив значения LE, DE и DL из формул (2), а также значение Л/=300 кГ, получим:

/?д = 275 кГ, F = m кГ.

Задача 1.7. Однородная налочка весом Р и длиной 1а опирается концом А о гладкую внутреннюю поверхность нолус()ери-ческой чаши радиуса г. Промежуточной точкой В налочка опирается о ребро чаши.

Определить величину угла а, образуемого палочкой с горнзоигом в положении равновесия, и опорные реакции в точках А п В. С - центр тяжести палочки, М - центр сферы, половина которой образует чашу фис. а).

Решение. Если опустить палочку концом А в полусферическую чашу, то она за{.мет в ней положение равновесия при некотором фиксированном значении угла я, образуемого палочкой с горизонтом. При этом угол я зависит от длины палочки 2а и радиуса чаши г.

В случае равновесия угол я долмсен быть таким, чтобы линии действия трех сил, приложенных

и - пересекались в одной точке. Реакцию направим по нормали к поверхности в дайной гочке, т. е. по радиусу AM, а реакцию - перпендикулярно к палочке (рис. б). Пусть О - точка пересечения линий действия этих трех сил. Такого построения оказывается достаточно для определения значения угла я. Рассматривая равнобедренный треугольник АМВ, имеем ЛЖ -Ж5= г, ВАМ = = Z ЛВМ. Так как £ МБА^ L BAS=ol, то £ ВАМ^ L АВМ = = я. Угол АВО, вписаншлй в окружность радиуса г, является по построению прямым. Он должен опираться на диаметр окружности; поэтому А0 = 2г. Из треугольника ЛОЛ находим Л5=ЛО-соз2я = = 2rcos2a. Из треугольника ACS имеем Л5= ЛС cos я = а cos я. (Так как центр тяжести однородной палочки расположен в ее середине, то АС=а.) Следовагельпо,

К задаче

к палочке, - веса Р и реакций R.

AS=2r cos 1(1. = а cos я.

а-\-у а'-г-Sir- COsa= Sr -

Для определения опорных реакций и Л„ построим замкнутый силовой треугольник (рис. в). Из произвольной точки К проводим век юр, равный силе Р. Проведя через начало вектора Р прямую /</:, параллельную реакции Л,р а через конец вектора Р - прямую LD, параллельную реакции К^, получим в точке пересечения этих прямых третью вершину N силового треугольника KLN. Из сравнения рис. б н в нетрудно видеть, что /1 NKL- 1 ВОС = о., / NLK= L QAM--= 90° - Z AfЛ5= 90° - 2я и, следовательно, /1 KNL = 180° - - (Z LKN-\- Z KLN) = <0°-\--x.

Применив к силовому треугольнику /CiAтеорему синусов, запишем:

sin (00°--а) Sin а S1I1 (90° - 2с()

R, = ptga, R, = P,

где cos а определяется по формуле (2).

Рекомендуем решить следующие задачи из Сборника задач но теоретической механике И. В. Мещерского, издания 1950 г. и последующих лет: 37, 38, 40, 41.

3°. Метод п р о е к ц и й. Ортогональная проекция силы иа ось, подобно проекции любого вектора на ось, равна произведению модуля силы на косинус угла, образованного положительным направлением оси проекций и направлением проектируемой силы (рис. 1.19):

ир f = Р cos (х, F).

Проекция силы на ось является алгебраической величиной. Если угол между положительным направлением оси проекций и векторо.м

Заменив cos 2а через 2cosa-1, получим:

2г (2 cos а - 1) = а cos а,

или

4г cos- а - а cos а. - 2г = 0.

Решив это квадратное уравнение, найдем:

а ± V-r 32г-=-- 8г -

Так как 0<a<ir/2, то 0<cosa<l. Поэтому, отбросив отрицательное значение cos а, окончательно получим:

1 2 3 4 5 ... 51